
题目列表(包括答案和解析)
(本小题满分8分)
设蚂蚁在如图正方体的表面沿棱爬行,它从一个顶点爬向另外三个顶点是等可能的,若蚂蚁的初始位置在顶点A,回答下列问题: 
(1)若爬了两条线段(线段可以重复爬行),写出蚂蚁经过的所有路径;
(2)若爬了两条线段(线段可以重复爬行),蚂蚁停在顶点C的概率是多少?
(3)若爬了三条线段(线段可以重复爬行),蚂蚁停在顶点G的概率是多少?
(本小题满分8分)
设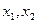 是关于
是关于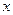 的一元二次方程
的一元二次方程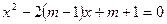 的两个实根,又
的两个实根,又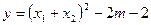 。
。
(Ⅰ)求 的取值范围;
的取值范围;
(Ⅱ)求 的解析式及最小值。
的解析式及最小值。
(本小题满分8分)设函数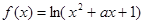 的定义域为
的定义域为 .
.
(Ⅰ)若 ,
, ,求实数
,求实数 的范围;
的范围;
(Ⅱ)若函数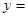
 的定义域为
的定义域为 ,求实数
,求实数 的取值范围.
的取值范围.
(本小题满分8分)设函数 的图象在
的图象在 处的切线方程为
处的切线方程为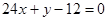 .
.
(Ⅰ)求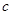 ,
,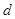 ;
;
(Ⅱ)若函数在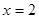 处取得极值
处取得极值 ,试求函数解析式并确定函数的单调区间.
,试求函数解析式并确定函数的单调区间.
(本小题满分8分)
设A ={x|x2+4x=0},B={x|x2+2(a+1)x+a2-1=0},其中x∈R,如果A∩B=B,求实数a的取值范围.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com