
题目列表(包括答案和解析)
(本小题满分8分)
已知,在△ABC中,∠BAC=90°,AB=AC,BC=![]() ,点D、E在BC边上(均不与点B、C重合,点D始终在点E左侧),且∠DAE=45°.
,点D、E在BC边上(均不与点B、C重合,点D始终在点E左侧),且∠DAE=45°.
1.(1)请在图①中找出两对相似但不全等的三角形,写在横线上 , ;
2.(2)设BE=m,CD=n,求m与n的函数关系式,并写出自变量n的取值范围;
3.(3)如图②,当BE=CD时,求DE的长;
4.(4)求证:无论BE与CD是否相等,都有DE2=BD2+CE2.

(本小题满分10分)已知,等腰Rt△ABC中,点O是斜边的中点,△MPN是直角三角形,固定△ABC,滑动△MPN,在滑动过程中始终保持点P在AC上,且 PM⊥AB,PN⊥BC,垂足分别为E、F.
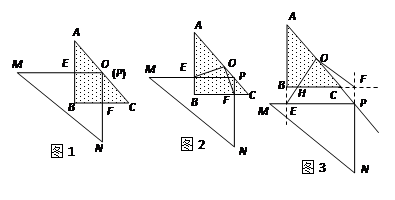
(1)如图1,当点P与点O重合时,OE、OF的数量和位置关系分别是____ __.
(2)当△MPN移动到图2的位置时,(1)中的结论还成立吗?请说明理由.
(3)如图3,等腰Rt△ABC的腰长为6,点P在AC的延长线上时,Rt△MPN的边PM
与AB的延长线交于点E,直线BC与直线NP交于点F,OE交BC于点H,且 EH: HO=2:5,则BE的长是多少?
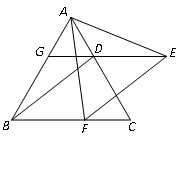
(本小题满分9分)已知:如图,△ABC是等边三角形,过AC边上的点D作DG∥BC,交AB于点G,在GD的延长线上取点E,使DE=DC,连接AE、BD.
(1)求证:△AGE≌△DAB;
(2)过点E作EF∥DB,交BC于点F,连AF,求∠AFE的度数.
 |
(本小题满分10分)
学习过三角函数,我们知道在直角三角形中,一个锐角的大小与两条边长的比值相互唯一确定,因此边长与角的大小之间可以相互转化.
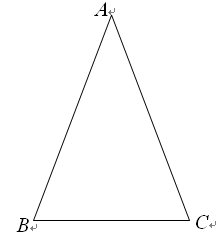
类似的,可以在等腰三角形中建立边角之间的联系,我们定义:等腰三角形中底边与腰的比叫做顶角的正对(sad).如图,在△ABC中,AB=AC,顶角A的正对记作sadA,这时sad A= .容易知道一个角的大小与这个角的正对值也是相互唯一确定的.
.容易知道一个角的大小与这个角的正对值也是相互唯一确定的.
根据上述对角的正对定义,解下列问题:
(1)sad ![]() 的值为( )A.
的值为( )A. ![]() B.1 C.
B.1 C. ![]() D.2
D.2
(2)对于![]() ,∠A的正对值sad A的取值范围是 .
,∠A的正对值sad A的取值范围是 .
(3)已知![]() ,其中
,其中![]() 为锐角,试求sad
为锐角,试求sad 的值.
的值.
(本小题满分5分)已知菱形纸片ABCD的边长为![]() ,∠A=60°,E为
,∠A=60°,E为![]() 边上的点,过点E作EF∥BD交AD于点F.将菱形先沿EF按图1所示方式折叠,点A落在点
边上的点,过点E作EF∥BD交AD于点F.将菱形先沿EF按图1所示方式折叠,点A落在点![]() 处,过点
处,过点![]() 作GH∥BD分别交线段BC、DC于点G、H,再将菱形沿GH按图1所示方式折叠,点C落在点
作GH∥BD分别交线段BC、DC于点G、H,再将菱形沿GH按图1所示方式折叠,点C落在点![]() 处,
处,![]() 与
与![]() H分别交
H分别交![]() 与
与![]() 于点M、N.若点
于点M、N.若点![]() 在△
在△![]() EF的内部或边上,此时我们称四边形
EF的内部或边上,此时我们称四边形![]() (即图中阴影部分)为“重叠四边形”.
(即图中阴影部分)为“重叠四边形”.
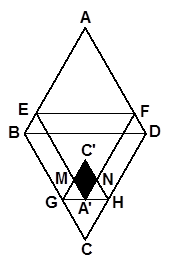


图1 图2 备用图
(1)若把菱形纸片ABCD放在菱形网格中(图中每个小三角形都是边长为1的等边三角形),点A、B、C、D、E恰好落在网格图中的格点上.如图2所示,请直接写出此时重叠四边形![]() 的面积;
的面积;
(2)实验探究:设AE的长为![]() ,若重叠四边形
,若重叠四边形![]() 存在.试用含
存在.试用含![]() 的代数式表示重叠四边形
的代数式表示重叠四边形![]() 的面积,并写出
的面积,并写出![]() 的取值范围(直接写出结果,备用图供实验,探究使用).
的取值范围(直接写出结果,备用图供实验,探究使用).
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com