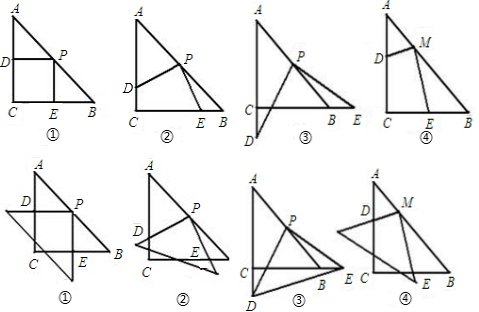
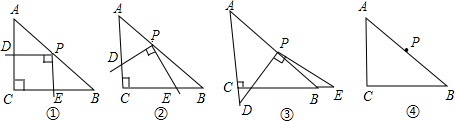
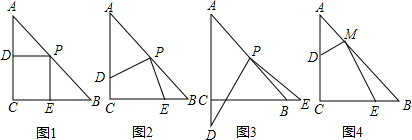
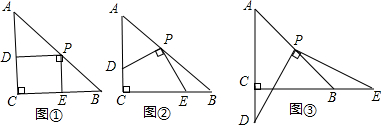
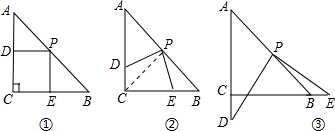
操作:在△ABC中,AC=BC=2,∠C=90°.将一块足够大的等腰直角三角板的直角顶点放在斜边AB的中点P处,将三角板绕点P旋转,三角板的两直角边分别交射线AC、CB于D、E两点.如图①②③是旋转三角板得到的图形中的3种情况.
(1)三角板绕点P旋转,当PD⊥AC时,如图①,四边形PDCE是正方形,则PD=PE.当PD与AC不垂直时,如图②、③,PD=PE还成立吗?并选择其中的一个图形证明你的结论.
(2)三角板绕点P旋转,△PEB是否成为等腰三角形?若能,求出此时CE的长;若不能,请说明理由.
(3)若将三角板的直角顶点放在斜边AB上的M处,且AM:MB=1:3,和前面一样操作,如图④,试问线段MD和ME之间有什么数量关系?并结合图形加以证明.