(2012•重庆模拟)草莓是对蔷薇科草莓属植物的通称,属多年生草本植物,草莓的外观呈心形,鲜美红嫩,果肉多汁,含有特殊的浓郁水果芳香,草莓营养价值高,含丰富维生素C,有帮助消化的功效,与此同时,草莓还可以巩固齿龈,清新口气,润泽喉部.我市某草莓种植基地去年第x个月种植草莓的亩数y(亩),与x(1≤x≤12,且x为整数)之间的函数关系如表:
| 月份x |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
| 13种植某数y |
6 |
8 |
10 |
12 |
14 |
16 |
16 |
16 |
16 |
16 |
16 |
16 |
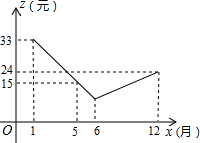
每亩收益z(元)与月份x(月)(1≤x≤12,且x为整数)之间存在如图所示的变化趋势:
(1)请观察题中的表格,用所学过的一次函数,反比例函数或二次函数的有关知识,直接写出y与x之间的函数关系式,根据如图所示的变化趋势,直接写出z与x之间满足的函数关系式;
(2)该草莓种植基地在去年哪个月的总收益最大,求出这个最大收益;
(3)今年1月份,该草莓种植基地加大规模,种植草莓比去年12月份多4亩,每亩收益比去年12月份多a%,今年2月份,该草莓种植基地继续加大规模,种植草莓比今年1月份多2a%,每亩收益比今年1月份多6元,若今年2月份该草莓种植基地总收益为672元,请你参考以下数据,通过计算估算出a的整数值.(参考数据:
=7.94,
=8.06,
=8.12)

 (2012•重庆模拟)草莓是对蔷薇科草莓属植物的通称,属多年生草本植物,草莓的外观呈心形,鲜美红嫩,果肉多汁,含有特殊的浓郁水果芳香,草莓营养价值高,含丰富维生素C,有帮助消化的功效,与此同时,草莓还可以巩固齿龈,清新口气,润泽喉部.我市某草莓种植基地去年第x个月种植草莓的亩数y(亩),与x(1≤x≤12,且x为整数)之间的函数关系如表:
(2012•重庆模拟)草莓是对蔷薇科草莓属植物的通称,属多年生草本植物,草莓的外观呈心形,鲜美红嫩,果肉多汁,含有特殊的浓郁水果芳香,草莓营养价值高,含丰富维生素C,有帮助消化的功效,与此同时,草莓还可以巩固齿龈,清新口气,润泽喉部.我市某草莓种植基地去年第x个月种植草莓的亩数y(亩),与x(1≤x≤12,且x为整数)之间的函数关系如表: 26、在长方形地块上建造公共绿地(图中阴影部分),其余的部分小路.根据图中的设计方案,利用你所学习的有关图形运动的知识,
26、在长方形地块上建造公共绿地(图中阴影部分),其余的部分小路.根据图中的设计方案,利用你所学习的有关图形运动的知识,