
题目列表(包括答案和解析)
| x |
| 2 |
| x+8 |
| 6 |
| x+1 |
| 3 |
|
解不等式与不等式组,并把解集在数轴上表示出来
(1) ≥
≥ (2)
(2)
| | C | D | 总计 |
| A | | | 200吨 |
| B | x吨 | | 300吨 |
| 总计 | 240吨 | 260吨 | 500吨 |
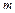 元(
元(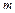 >0),其余线路的运费不变,试讨论总运费最小的调运方案.
>0),其余线路的运费不变,试讨论总运费最小的调运方案.(12分)“5·12”四川汶川大地震的灾情牵动全国人民的心,某市A、B两个蔬菜基地得知四川C、D两个灾民安置点分别急需蔬菜240吨和260吨的消息后,决定调运蔬菜支援灾区.已知A蔬菜基地有蔬菜200吨,B蔬菜基地有蔬菜300吨,现将这些蔬菜全部调往C、D两个灾民安置点.从A地运往C、D两处的费用分别为每吨20元和25元,从B地运往C、D两处的费用分别为每吨15元和18元.设从B地运往C处的蔬菜为x吨.
请填写下表,并求两个蔬菜基地调运蔬菜的运费相等时x的值;
|
| C | D | 总计 |
| A |
|
| 200吨 |
| B | x吨 |
| 300吨 |
| 总计 | 240吨 | 260吨 | 500吨 |
(1)设A、B两个蔬菜基地的总运费为w元,写出w与x之间的关系式,并求总运费最小的调运方案;
(2)经过抢修,从B地到C处的路况得到进一步改善,缩短了运输时间,运费每吨减少![]() 元(
元(![]() >0),其余线路的运费不变,试讨论总运费最小的调运方案.
>0),其余线路的运费不变,试讨论总运费最小的调运方案.
(3)不等式与不等式组参考答案仅供参考
(12分)“5·12”四川汶川大地震的灾情牵动全国人民的心,某市A、B两个蔬菜基地得知四川C、D两个灾民安置点分别急需蔬菜240吨和260吨的消息后,决定调运蔬菜支援灾区.已知A蔬菜基地有蔬菜200吨,B蔬菜基地有蔬菜300吨,现将这些蔬菜全部调往C、D两个灾民安置点.从A地运往C、D两处的费用分别为每吨20元和25元,从B地运往C、D两处的费用分别为每吨15元和18元.设从B地运往C处的蔬菜为x吨.
请填写下表,并求两个蔬菜基地调运蔬菜的运费相等时x的值;
|
|
C |
D |
总计 |
|
A |
|
|
200吨 |
|
B |
x吨 |
|
300吨 |
|
总计 |
240吨 |
260吨 |
500吨 |
(1)设A、B两个蔬菜基地的总运费为w元,写出w与x之间的关系式,并求总运费最小的调运方案;
(2)经过抢修,从B地到C处的路况得到进一步改善,缩短了运输时间,运费每吨减少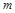 元(
元(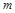 >0),其余线路的运费不变,试讨论总运费最小的调运方案.
>0),其余线路的运费不变,试讨论总运费最小的调运方案.
(3)不等式与不等式组参考答案仅供参考
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com