题目列表(包括答案和解析)
我们做如下的规定：如果一个三角形在运动变化时保持形状和大小不变，则把这样的三角形称为三角形板．
把两块边长为4的等边三角形板ABC和DEF叠放在一起，使三角形板DEF的顶点D与三角形板ABC的AC边中点O重合，把三角形板ABC固定不动，让三角形板DEF绕点O旋转，设射线DE与射线AB相交于点M，射线DF与线段BC相交于点N．
(1)如图1，当射线DF经过点B，即点Q与点B重合时，易证△ADM∽△CND．此时，AM·CN＝________．
(2)将三角形板DEF由图1所示的位置绕点O沿逆时针方向旋转，设旋转角为α．其中0°＜α＜90°，问AM·CN的值是否改变？说明你的理由．
(3)在(2)的条件下，设AM＝x，两块三角形板重叠面积为y，求y与x的函数关系式．(图2，图3供解题用)
| AB |
| AB |
| AB |
．| OA |
| OA |
| OA |
| OB |
| 3 |
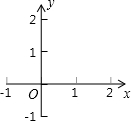
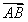，线段AB的长度叫做有向线段的长度（或模），记作
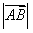。有向线段包含三个要素、始点、方向和长度，知道了有向线段的始点，它的终点就被方向和长度惟一确定。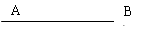
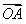（有向线段与轴的长度单位相同），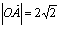
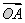与x轴的正半轴的夹角是45。； 
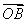的终点B的坐标为（3，
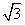），求它的模及它与x轴的正半轴的夹角的度数
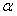。 （本题满分8分）先阅读读短文，再解答短文后面的问题：
在几何学中，通常用点表示位置，用线段的长度表示两点间的距离，用一条射线表示一个方向。在线段的两个端点中（如图），如果我们规定一个顺序：
为始点，
为终点，我们就说线段
具有射线的方向，线段叫做有向线段，记作
，线段的长度叫做有向线段的长度（或模），记作
。
有向线段包含三个要素：始点、方向和长度，知道了有向线段的始点，它的终点就被方向和长度一确定。解答下列问题：
1.（1）在平面直角坐标系中画出有向线段
（有向线段与
轴的长度单位相同），
，与轴的正半轴的夹角是
，且与
轴的正半轴的夹角是；
2.（2）若
的终点的坐标为（3，
），求它的模及它与轴的正半轴的夹角
的度数。
在几何学中，通常用点表示位置，用线段的长度表示两点间的距离，用一条射线表示一个方向。在线段的两个端点中（如图），如果我们规定一个顺序：
为始点，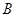
为终点，我们就说线段
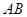具有射线的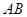方向，线段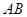叫做有向线段，记作
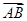，线段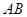的长度叫做有向线段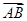的长度（或模），记作
。
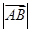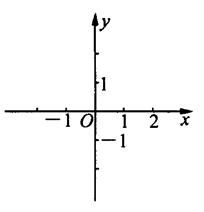
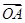（有向线段与
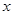轴的长度单位相同），
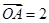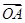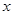，与轴的正半轴的夹角是
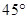，且与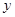
轴的正半轴的夹角是；
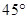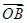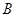的终点的坐标为（3，
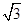），求它的模及它与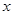轴的正半轴的夹角
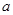的度数。湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com