
题目列表(包括答案和解析)
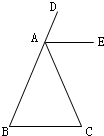 24、根据图形填空:
24、根据图形填空: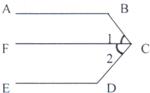 29、如图,根据图形填空:
29、如图,根据图形填空: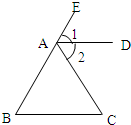 22、根据图形及题意填空,并在括号里写上理由.
22、根据图形及题意填空,并在括号里写上理由.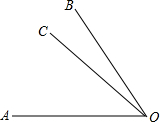 下面是小民解的一道题,请你检查他的解答情况.
下面是小民解的一道题,请你检查他的解答情况. 如图,甲、乙二人分别从长为100米、宽为50米的矩形广场的边缘点A、C两点同时出发,甲由A点向D点运动,速度为2米/秒,乙由C点向B点运动,速度为3米/秒.设x秒后两人直线距离是60米.
如图,甲、乙二人分别从长为100米、宽为50米的矩形广场的边缘点A、C两点同时出发,甲由A点向D点运动,速度为2米/秒,乙由C点向B点运动,速度为3米/秒.设x秒后两人直线距离是60米.湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com