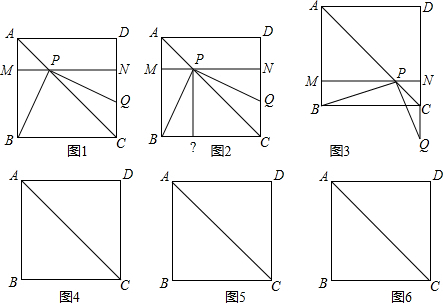
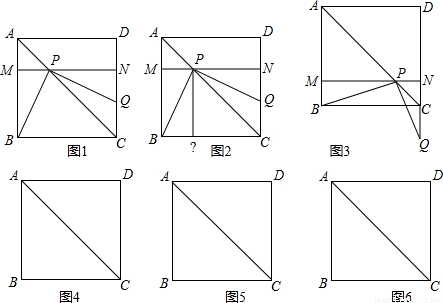
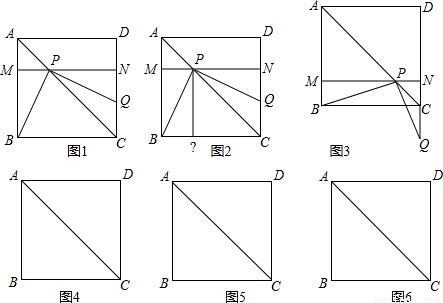
操作:将一把三角尺放在边长为1的正方形ABCD上,并使它的直角顶点P在对角线AC上滑动,直角的一边始终经过点B,另一边与射线DC相交于点Q.
探究:设A、P两点间的距离为x.
(1)点Q在CD上时,线段PQ与线段PB之间有怎样的大小关系?试证明你观察得到的结论(如图1);
(2)点Q边CD上时,设四边形PBCQ的面积为y,求y与x之间的函数解析式,并写出函数的定义域(如图2);
(3)点P在线段AC上滑动时,△PCQ是否可能成为等腰三角形?如果可能,指出所有能使△PCQ成为等腰三角形的点Q的位置,并求出相应的x的值;如果不可能,试说明理由(如图3).(图4、图5、图6的形状、大小相同,图4供操作、实验用,图5和图6备用).