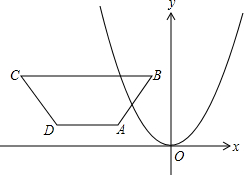
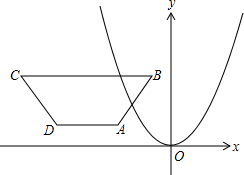
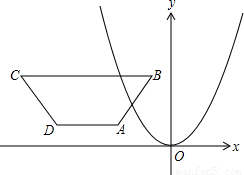
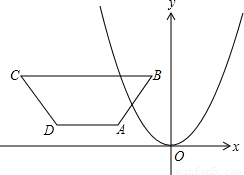
如图，在直角坐标系内，已知等腰梯形ABCD，AD∥BC∥x轴，AB=CD，AD=2，BC=8，AB=5，B点的坐标是（-1，5）．
（1）直接写出下列各点坐标．A（，）C（，）D（，）；
（2）等腰梯形ABCD绕直线BC旋转一周形成的几何体的表面积（保留π）；
（3）直接写出抛物线y=x²左右平移后，经过点A的函数关系式；
（4）若抛物线y=x²可以上下左右平移后，能否使得A，B，C，D四点都在抛物线上？若能，请说理由；若不能，将“抛物线y=x²”改为“抛物线y=mx²”，试确定m的值，使得抛物线y=mx²经过上下左右平移后能同时经过A，B，C，D四点．