
题目列表(包括答案和解析)
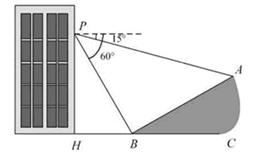
(本题满分5分)如图,小明在大楼30米高
(即PH=30米)的窗口P处进行观测,测得山
坡上A处的俯角为15°,山脚B处的俯角为
60°,已知该山坡的坡度i(即tan∠ABC)为1:
,点P、H、B、C、A在同一个平面上.点
H、B、C在同一条直线上,且PH⊥HC.
(1)山坡坡角(即∠ABC)的度数等于 ▲ 度;
(2)求A、B两点间的距离(结果精确到0.1米,参考数据:≈1.732).
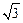 ,点P、H、B、C、A在同一个平面上.点
,点P、H、B、C、A在同一个平面上.点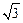 ≈1.732).
≈1.732).(本题满分5分)如图,小明在大楼30米高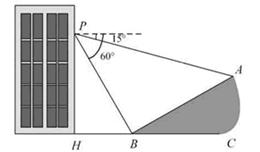
(即PH=30米)的窗口P处进行观测,测得山
坡上A处的俯角为15°,山脚B处的俯角为
60°,已知该山坡的坡度i(即tan∠ABC)为1: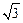 ,点P、H、B、C、A在同一个平面上.点
,点P、H、B、C、A在同一个平面上.点
H、B、C在同一条直线上,且PH⊥HC.
(1)山坡坡角(即∠ABC)的度数等于 ▲ 度;
(2)求A、B两点间的距离(结果精确到0.1米,参考数据: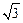 ≈1.732).
≈1.732).
(本题满分5分)如图,小明在大楼30米高
(即PH=30米)的窗口P处进行观测,测得山
坡上A处的俯角为15°,山脚B处的俯角为
60°,已知该山坡的坡度i(即tan∠ABC)为1:
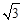 ,点P、H、B、C、A在同一个平面上.点
,点P、H、B、C、A在同一个平面上.点
H、B、C在同一条直线上,且PH⊥HC.
(1)山坡坡角(即∠ABC)的度数等于 ▲ 度;
(2)求A、B两点间的距离(结果精确到0.1米,参考数据: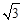 ≈1.732).
≈1.732).
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com