
题目列表(包括答案和解析)
 变,若BE=CF的结论仍然成立,请写出△AEF必须满足的条件,并加以证明.
变,若BE=CF的结论仍然成立,请写出△AEF必须满足的条件,并加以证明.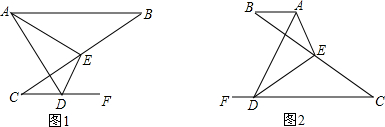
 9、如图,已知?ABCD的对角线交于O,过O作直线交AB、CD的反向延长线于E、F,求证:OE=OF.
9、如图,已知?ABCD的对角线交于O,过O作直线交AB、CD的反向延长线于E、F,求证:OE=OF.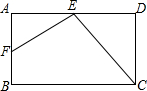 如图,在矩形ABCD中,E为AD的中点,过E作直线交AB于F.当EF与CE满足何条件时,△AEF与△CDE相似?并说明理由.
如图,在矩形ABCD中,E为AD的中点,过E作直线交AB于F.当EF与CE满足何条件时,△AEF与△CDE相似?并说明理由.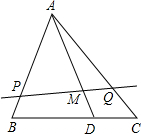 如图所示,在△ABC中,已知BD=2DC,AM=3MD,过M作直线交AB,AC于P、Q两点.则
如图所示,在△ABC中,已知BD=2DC,AM=3MD,过M作直线交AB,AC于P、Q两点.则| AB |
| AP |
| 2AC |
| AQ |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com