
题目列表(包括答案和解析)
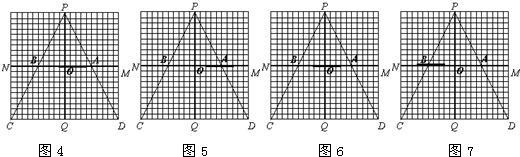
 )以每秒1个单位长的速度在铁路线MN上通过时,列车将阻挡王凯的部分视线,在区域MNCD内形成盲区(不考虑列车的宽度和车厢间的缝隙).设列车车头运行到M点的时刻为0,列车从M点向N点方向运行的时间为t(秒).
)以每秒1个单位长的速度在铁路线MN上通过时,列车将阻挡王凯的部分视线,在区域MNCD内形成盲区(不考虑列车的宽度和车厢间的缝隙).设列车车头运行到M点的时刻为0,列车从M点向N点方向运行的时间为t(秒).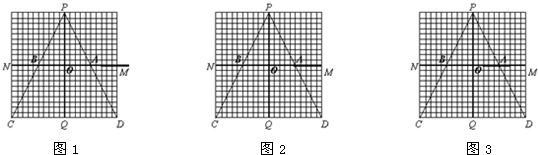
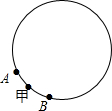 如图,A和B两个小机器人,自甲处同时出发相背而行,绕直径为整数米的圆周上运动,15分钟内相遇7次,如果A的速度每分钟增加6米,则A和B在15分钟内相遇9次,问圆周直径至多是多少米?至少是多少米?(取π=3.14)
如图,A和B两个小机器人,自甲处同时出发相背而行,绕直径为整数米的圆周上运动,15分钟内相遇7次,如果A的速度每分钟增加6米,则A和B在15分钟内相遇9次,问圆周直径至多是多少米?至少是多少米?(取π=3.14) 如图,△ABE和△ADC是△ABC分别沿AB,AC边翻折180°形成的,∠1=140°,∠2=25°,∠3=15°,则∠α的度数为
如图,△ABE和△ADC是△ABC分别沿AB,AC边翻折180°形成的,∠1=140°,∠2=25°,∠3=15°,则∠α的度数为
 )以每秒1个单位长的速度在铁路线MN上通过时,列车将阻挡王凯的部分视线,在区域MNCD内形成盲区(不考虑列车的宽度和车厢间的缝隙).设列车车头运行到M点的时刻为0,列车从M点向N点方向运行的时间为t(秒).
)以每秒1个单位长的速度在铁路线MN上通过时,列车将阻挡王凯的部分视线,在区域MNCD内形成盲区(不考虑列车的宽度和车厢间的缝隙).设列车车头运行到M点的时刻为0,列车从M点向N点方向运行的时间为t(秒).

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com