现将3只相同的油桶运往外地，为了确保运输安全，这3只油桶须紧贴在一起，于是，爱动脑筋的小青和小银分别想出了自己的处理方法．
小青：“用截面为等边三角形的铁桶将3只油桶紧紧地套住”（如图①）．
小银：“用截面为圆的铁桶将3只油桶紧紧地箍住”．（如图②）

假设油桶的外径为2a，铁桶的高度都等于油桶的高度．
（1）试通过计算分析，小青和小银的想法哪一种更省料；
（2）他们的朋友小猴又想出另一种方法：“用孙悟空的金箍棒夹在它们的中间将3只油桶粘住”（如图③），他这一设想能否实现？若能实现，金箍棒的直径是多少最适宜？

（3）你有没有更合理的方法？如果有，请予以说明；
（4）经历这一课题的实践与探索过程，你有什么感受？

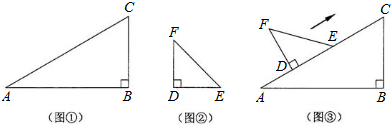
刘卫同学在一次课外活动中，用硬纸片做了两个直角三角形，见图①、②．图①中，∠B=90°，∠A=30°，BC=6cm；图②中，∠D=90°，∠E=45°，DE=4cm．图③是刘卫同学所做的一个实验：他将△DEF的直角边DE与△ABC的斜边AC重合在一起，并将△DEF沿AC方向移动．在移动过程中，D、E两点始终在AC边上（移动开始时点D与点A重合）．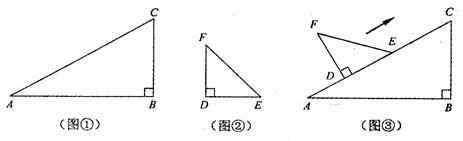
（1）在△DEF沿AC方向移动的过程中，刘卫同学发现：F、C两点间的距离逐渐．（填“不变”、“变大”或“变小”）
（2）刘卫同学经过进一步地研究，编制了如下问题：
问题①：当△DEF移动至什么位置，即AD的长为多少时，F、C的连线与AB平行？
问题②：当△DEF移动至什么位置，即AD的长为多少时，以线段AD、FC、BC的长度为三边长的三角形是直角三角形？
问题③：在△DEF的移动过程中，是否存在某个位置，使得∠FCD=15°？如果存在，求出AD的长度；如果不存在，请说明理由．
请你分别完成上述三个问题的解答过程．