如图17－1－9所示，已知直线y₁=x+m与x轴、y轴分别交于点A、B，与双曲线y₂= （k<0）分别交于点C、D，且C点坐标为（－1，2）.

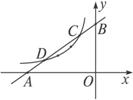
图17－1－9

（1）分别求直线AB与双曲线的解析式；

（2）求出点D的坐标；

（3）利用图象直接写出当x在什么范围内时，y₁>y₂.

如图13所示，已知点P在∠AOC的边OA上，

（1）过点P画OA的垂线交OC于点B；

（2）画点P到OB的垂线段PM；

（3）在上述画图中，哪一条线段的长表示点P到OB边上的距离？

（4）比较PM与OP的大小，并说明理由．

 

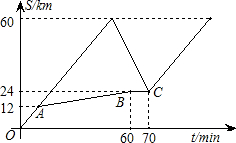有六名学生分成甲、乙两组（每组三个人），分乘两辆出租车同时从学校出发去世博园参观，出发10分钟后有一辆汽车出现故障，接着正常行驶的一辆车先把第一批学生送到世博园再回头接第二批学生，同时第二批学生步行前往．设出发后t分钟时汽车离开学校的路程为s千米，函数关系如图所示，第二批学生步行过程中离开学校的路程与出发时间t的图象如图中折线段AB-BC所示．（假设汽车载人和空载时的速度分别保持不变，学生步行速度不变，学生上下车时间忽略不计．）
（1）从学校出发到全体到达世博园共花了分钟；
（2）请解释图中线段BC的实际意义；
（3）为了节省时间，小明提出了一个想法：从故障点开始，在第二批学生步行的同时出租车先把第一批学生送到途中放下，让他们步行，再回头接第二批学生，使得两批学生同时到达博物馆．如果这样，学生在整个步行过程中不能休息，但步行的平均速度就会减少0.04km/min，请问按这种想法能提前多少分钟到达世博园？（假设汽车载人和空载时的速度分别保持不变．）