
题目列表(包括答案和解析)

【改编】(本小题满分10分)
数形结合作为一种数学思想方法,数形结合的应用大致又可分为两种情形:或者借助于数的精确性来阐明形的某些属性,即“以数解形”;或者借助形的 几何直观性来阐明数之间的某种关系,即“以形助数”。 如浙教版九上课本第109页作业题第2题:如图1,已知在△ABC中,∠ACB=900,CD⊥AB,D为垂足。易证得两个结论:(1)AC·BC = AB·CD (2)AC2= AD·AB
几何直观性来阐明数之间的某种关系,即“以形助数”。 如浙教版九上课本第109页作业题第2题:如图1,已知在△ABC中,∠ACB=900,CD⊥AB,D为垂足。易证得两个结论:(1)AC·BC = AB·CD (2)AC2= AD·AB
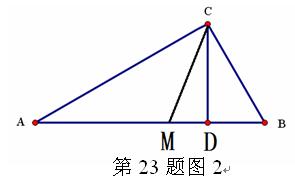
(1)请你用数形结合的“以数解形”思想来解:如图2,已知在△ABC中(AC>BC),∠ACB=900,CD⊥AB,D为垂足, CM平分∠ACB,且BC、AC是方程x2-14x+48=0的两个根,求AD、MD的长。
(2)请你用数形结合的“以形助数”思想来解:设a、b、c、d都是正数,满足a:b=c:d,且a最大。求证:a+d>b+c(提示:不访设AB=a,CD=d,AC=b,BC=c,构造图1)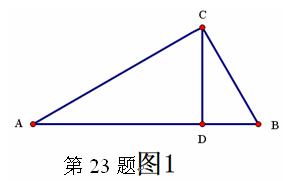
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com