
题目列表(包括答案和解析)
 (2012•柳州)如图,在△ABC中,AB=2,AC=BC=
(2012•柳州)如图,在△ABC中,AB=2,AC=BC=| 5 |
| 1 |
| 2 |
| 3 |
| 3 |
| 3 |
| 3 |
| x2-2 |
| x2-2 |
| 4 |
| x |
| 4 |
| x |
| ab |
| 4 |
| x |
x×
|
| 4 |
| x |
| ||
| 2 |
| ||
| 2 |
| 3 |
| x |
| 6 |
| 6 |
| x |
| x2-2x+9 |
 △ABC中,AB=2,AC=BC= 5 .
△ABC中,AB=2,AC=BC= 5 .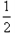 S△ABC;
S△ABC;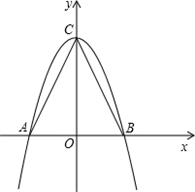
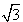 ,y4=-
,y4=-  .所以,原方程的解是y1=1,y2=-1,y3=
.所以,原方程的解是y1=1,y2=-1,y3= 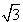 ,
,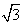 ,再如
,再如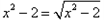 ,可设
,可设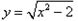 ,用同样的方法也可求解.
,用同样的方法也可求解.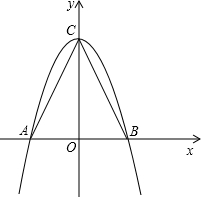 如图,在△ABC中,AB=2,AC=BC=
如图,在△ABC中,AB=2,AC=BC= .
. S△ABC;
S△ABC; ,y4=-
,y4=- .
. ,y4=-
,y4=- .
.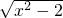 ,可设y=
,可设y=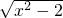 ,用同样的方法也可求解.
,用同样的方法也可求解.如图,在△ABC中,AB=2,AC=BC= 5 .
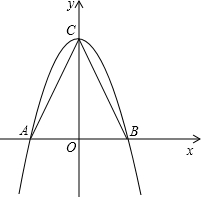
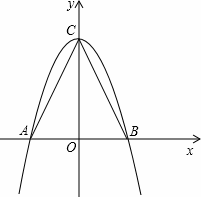
(1)以AB所在的直线为x轴,AB的垂直平分线为y轴,建立直角坐标系如图,请你分别写出A、B、C三点的坐标;
(2)求过A、B、C三点且以C为顶点的抛物线的解析式;
(3)若D为抛物线上的一动点,当D点坐标为何值时,S△ABD=![]() S△ABC;
S△ABC;
(4)如果将(2)中的抛物线向右平移,且与x轴交于点A′B′,与y轴交于点C′,当平移多少个单位时,点C′同时在以A′B′为直径的圆上(解答过程如果有需要时,请参看阅读材料).
附:阅读材料
一元二次方程常用的解法有配方法、公式法和因式分解法,对于一些特殊方程可以通过换元法转化为一元二次方程求解.如解方程:y4-4y2+3=0.
解:令y2=x(x≥0),则原方程变为x2-4x+3=0,解得x1=1,x2=3.
当x1=1时,即y2=1,∴y1=1,y2=-1.
当x2=3,即y2=3,∴y3= 3 ,y4=- 3 .
所以,原方程的解是y1=1,y2=-1,y3= 3 ,y4=- 3 .
再如![]() ,可设
,可设![]() ,用同样的方法也可求解.
,用同样的方法也可求解.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com