练习册

  • 练习册
  • 试题
    三角形相似的判定和性质 (1)三角形相似的判定方法有 . . .直角三角形全等的判定除了上述方法外.还有 . (2)相似三角形的 相等. 成比例. 等于相似比. 等于相似比的平方. 【查看更多】

     

    题目列表(包括答案和解析)

       如图，边长为4的等边三角形AOB的顶点O在坐标原点，点A在x轴正半轴上，点B在第一象限．一动点P沿x轴以每秒1个单位长的速度向点A匀速运动，当点P到达点A时停止运动，设点P运动的时间是t秒．将线段BP的中点绕点P按顺时针方向旋转60°得点C，点C随点P的运动而运动，连接CP、CA，过点P作PD⊥OB于点D．

    （1）填空：PD的长为               （用含t的代数式表示）；

    （2）求点C的坐标（用含t的代数式表示）；

    （3）在点P从O向A运动的过程中，△PCA能否成为直角三角形？若能，求t的值．若不能，请说明理由；

    （4）填空：在点P从O向A运动的过程中，点C运动路线的长为                            

    【解析】此题考核相似三角形的判定和性质，旋转的性质

     

    查看答案和解析>>

       如图，边长为4的等边三角形AOB的顶点O在坐标原点，点A在x轴正半轴上，点B在第一象限．一动点P沿x轴以每秒1个单位长的速度向点A匀速运动，当点P到达点A时停止运动，设点P运动的时间是t秒．将线段BP的中点绕点P按顺时针方向旋转60°得点C，点C随点P的运动而运动，连接CP、CA，过点P作PD⊥OB于点D．

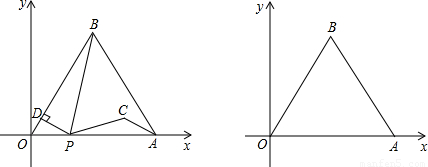
    （1）填空：PD的长为                （用含t的代数式表示）；

    （2）求点C的坐标（用含t的代数式表示）；

    （3）在点P从O向A运动的过程中，△PCA能否成为直角三角形？若能，求t的值．若不能，请说明理由；

    （4）填空：在点P从O向A运动的过程中，点C运动路线的长为                             

    【解析】此题考核相似三角形的判定和性质，旋转的性质

     

    查看答案和解析>>

    八年级数学学习合作小组在学过《图形的相似》这一章后，发现可将相似三角形的定义、判定以及性质拓展到矩形、菱形的相似中去．如：我们可以定义：“长和宽之比相等的矩形是相似矩形．”相似矩形也有以下的性质：相似矩形的对角线之比等于相似比，周长比等于相似比，面积比等于相似比的平方等等．请你参与这个学习小组，一同探索这类问题：
    （1）写出判定菱形相似的一种判定方法：若有一组角对应相等（或两组对角线对应成比例），则这两个菱形相似；
    （2）如图，将菱形ABCD沿着直线AC向右平移后得到菱形A′B′C′D′，试证明：四边形A′FCE是菱形，且菱形ABCD∽菱形A′FCE；
    （3）若AC=
    		2
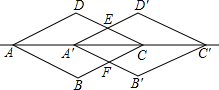
    ，菱形A′FCE的面积是菱形ABCD面积的一半，求平移的距离AA′的长．精英家教网

    查看答案和解析>>

    某校研究性学习小组在研究相似图形时，发现相似三角形的定义、判定及其性质，可以拓展到扇形的相似中去.例如，可以定义：“圆心角相等且半径和弧长对应成比例的两个扇形叫做相似扇形”；相似扇形有性质：弧长比等于半径比，面积比等于半径比的平方….请你协助他们探索这个问题.

    (1)写出判定扇形相似的一种方法：若__________________________，则两个扇形相似；

    (2)有两个圆心角相等的扇形，其中一个半径为a、弧长为m，另一个半径为2a，则它的弧长为________________________；

    (3)图(1)是一完全打开的纸扇，外侧两竹条AB和AC的夹角为120°，AB为30 cm，现要做一个和它形状相同、面积是它一半的纸扇〔如图(2)〕，求新做纸扇(扇形)的圆心角和半径.

    查看答案和解析>>

    如图，在平行四边形ABCD中，过点A作AE⊥BC，垂足为E，连接DE，F为线段DE上一点，且∠AFE＝∠B.

    （1）求证：∠DAF＝∠CDE

    （2）问△ADF与△DEC相似吗？为什么？

    （3）若AB＝4,AD＝3,AE＝3,求AF的长.

    【解析】此题考核平行四边形的性质，相似三角形的判定和性质

     

    查看答案和解析>>


    同步练习册答案