
题目列表(包括答案和解析)
| 3 |
| 1 | ||
2+
|
 ≈1.7,tan15°=
≈1.7,tan15°= )
) 
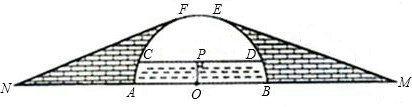
某河道上有一个半圆形的拱桥,河两岸筑有拦水堤坝,其半圆形桥洞的横截面如图所示.已知上、下桥的坡面线ME、NF与半圆相切,上、下桥斜面的坡度i=1∶3.7,桥下水深OP=5米,水面宽度CD=24米.设半圆的圆心为O,直径AB在坡角顶点M、N的连线上,求从M点上坡、过桥、下坡到N点的最短路径长.(参考数据:π≈3,![]() ≈1.7,tan15°=
≈1.7,tan15°=![]()

某河道上有一个半圆形的拱桥,河两岸筑有拦水堤坝,其半圆形桥洞的横截面如图所示.已知上、下桥的坡面线ME、NF与半圆相切,上、下桥斜面的坡度i=1:3.7,桥下水深OP=5米,水面宽度CD=24米.设半圆的圆心为O,直径AB在直角顶点M、N的连线上,求从M点上坡、过桥、下坡到N点的最短路径长.(参考数据:![]() ,
,![]() ,
,![]() )
)

 ≈1.7,tan15°=
≈1.7,tan15°= )
)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com