A.40                 B.30                   C.20                    D.12

普通高中新课程标准实验教科书（数学必修3）知识结构框图如下，则空白的框内应该填入（    ）

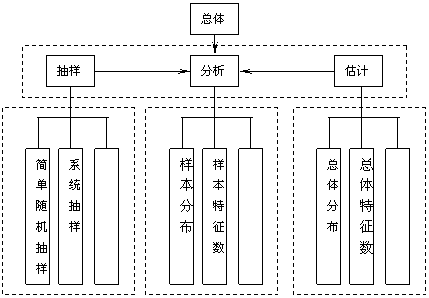A．分层抽样、相关关系、相关系数      B．分层抽样、相关系数、相关关系

C．相关关系、分层抽样、相关系数      D．相关系数、相关关系、分层抽样

2007年是某省实施新课程改革后的第一次高考，经教育部批准该省自主命题，为慎重起见，该省于2005年制定了两套高考方案，且对这两套方案在全省14个地级市分别召集专家进行研讨，并对认为合理的方案进行了投票表决，统计结果如下：

第一套方案：38，25，73，64，20，55，72，41，8，67，70，66，58，24

第二套方案：36，42，6，61，21，54，12，42，5，14，19，19，45，37

用茎叶图说明哪个方案比较稳妥．