
题目列表(包括答案和解析)
(2009全国卷Ⅱ文)(本小题满分12分)
|
|
(Ⅰ)求a,b的值;
(Ⅱ)C上是否存在点P,使得当l绕F转到某一位置时,有![]() 成立?
成立?
若存在,求出所有的P的坐标与l的方程;若不存在,说明理由。
解析:本题考查解析几何与平面向量知识综合运用能力,第一问直接运用点到直线的距离公式以及椭圆有关关系式计算,第二问利用向量坐标关系及方程的思想,借助根与系数关系解决问题,注意特殊情况的处理。
(2009全国卷Ⅱ文)(本小题满分12分)
|
|
(Ⅰ)求a,b的值;
(Ⅱ)C上是否存在点P,使得当l绕F转到某一位置时,有![]() 成立?
成立?
若存在,求出所有的P的坐标与l的方程;若不存在,说明理由。
解析:本题考查解析几何与平面向量知识综合运用能力,第一问直接运用点到直线的距离公式以及椭圆有关关系式计算,第二问利用向量坐标关系及方程的思想,借助根与系数关系解决问题,注意特殊情况的处理。
某港口的水深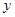 (米)是时间
(米)是时间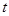 (
(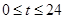 ,单位:小时)的函数,下面是每天时间与水深的关系表:
,单位:小时)的函数,下面是每天时间与水深的关系表:
|
|
0 |
3 |
6 |
9 |
12 |
15 |
18 |
21 |
24 |
|
|
10 |
13 |
9.9 |
7 |
10 |
13 |
10.1 |
7 |
10 |
经过长期观测, 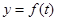 可近似的看成是函数
可近似的看成是函数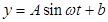 ,(本小题满分14分)
,(本小题满分14分)
(1)根据以上数据,求出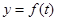 的解析式。
的解析式。
(2)若船舶航行时,水深至少要11.5米才是安全的,那么船舶在一天中的哪几段时间可以安全的进出该港?
【解析】第一问由表中数据可以看到:水深最大值为13,最小值为7,,
∴A+b=13, -A+b=7 解得 A=3, b=10
第二问要想船舶安全,必须深度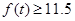 ,即
,即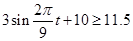
∴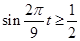
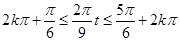
解得:
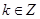 得到结论。
得到结论。
已知点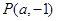 (
( ),过点
),过点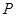 作抛物线
作抛物线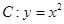 的切线,切点分别为
的切线,切点分别为 、
、 (其中
(其中 ).
).
(Ⅰ)若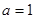 ,求
,求 与
与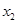 的值;
的值;
(Ⅱ)在(Ⅰ)的条件下,若以点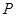 为圆心的圆
为圆心的圆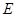 与直线
与直线 相切,求圆
相切,求圆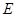 的方程;
的方程;
(Ⅲ)若直线 的方程是
的方程是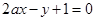 ,且以点
,且以点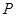 为圆心的圆
为圆心的圆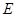 与直线
与直线 相切,
相切,
求圆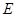 面积的最小值.
面积的最小值.
【解析】本试题主要考查了抛物线的的方程以及性质的运用。直线与圆的位置关系的运用。
中∵直线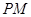 与曲线
与曲线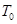 相切,且过点
相切,且过点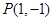 ,∴
,∴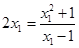 ,利用求根公式得到结论先求直线
,利用求根公式得到结论先求直线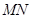 的方程,再利用点P到直线的距离为半径,从而得到圆的方程。
的方程,再利用点P到直线的距离为半径,从而得到圆的方程。
(3)∵直线 的方程是
的方程是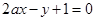 ,
,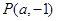 ,且以点
,且以点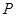 为圆心的圆
为圆心的圆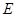 与直线
与直线 相切∴点
相切∴点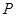 到直线
到直线 的距离即为圆
的距离即为圆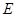 的半径,即
的半径,即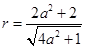 ,借助于函数的性质圆
,借助于函数的性质圆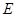 面积的最小值
面积的最小值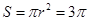
(Ⅰ)由 可得,
可得,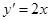 . ------1分
. ------1分
∵直线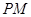 与曲线
与曲线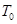 相切,且过点
相切,且过点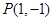 ,∴
,∴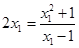 ,即
,即 ,
,
∴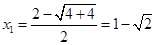 ,或
,或 , --------------------3分
, --------------------3分
同理可得: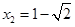 ,或
,或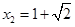 ----------------4分
----------------4分
∵ ,∴
,∴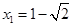 ,
,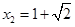 . -----------------5分
. -----------------5分
(Ⅱ)由(Ⅰ)知, ,
, ,则
,则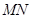 的斜率
的斜率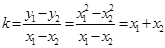 ,
,
∴直线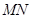 的方程为:
的方程为: ,又
,又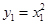 ,
,
∴ ,即
,即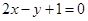 . -----------------7分
. -----------------7分
∵点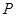 到直线
到直线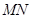 的距离即为圆
的距离即为圆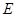 的半径,即
的半径,即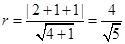 ,--------------8分
,--------------8分
故圆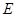 的面积为
的面积为 . --------------------9分
. --------------------9分
(Ⅲ)∵直线 的方程是
的方程是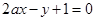 ,
,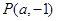 ,且以点
,且以点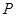 为圆心的圆
为圆心的圆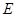 与直线
与直线 相切∴点
相切∴点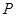 到直线
到直线 的距离即为圆
的距离即为圆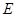 的半径,即
的半径,即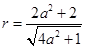 , ………10分
, ………10分
∴
 ,
,
当且仅当 ,即
,即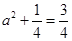 ,
,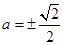 时取等号.
时取等号.
故圆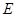 面积的最小值
面积的最小值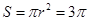 .
.
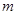 ,
,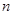 ,
,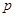 为常数,离心率为
为常数,离心率为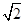 的双曲线
的双曲线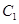 :
: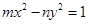 上的动点
上的动点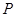 到两焦点的距离之和的最小值为
到两焦点的距离之和的最小值为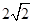 ,抛物线
,抛物线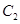 :
: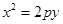
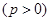 的焦点与双曲线
的焦点与双曲线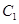 的一顶点重合。(Ⅰ)求抛物线
的一顶点重合。(Ⅰ)求抛物线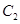 的方程;(Ⅱ)过直线
的方程;(Ⅱ)过直线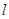 :
: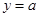 (
(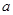 为负常数)上任意一点
为负常数)上任意一点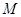 向抛物线
向抛物线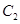 引两条切线,切点分别为
引两条切线,切点分别为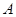 、
、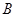 ,坐标原点
,坐标原点 恒在以
恒在以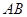 为直径的圆内,求实数
为直径的圆内,求实数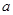 的取值范围。
的取值范围。
【解析】第一问中利用由已知易得双曲线焦距为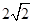 ,离心率为
,离心率为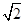 ,则长轴长为2,故双曲线的上顶点为
,则长轴长为2,故双曲线的上顶点为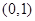 ,所以抛物线
,所以抛物线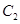 的方程
的方程
第二问中,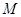 为
为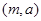 ,
,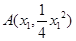 ,
, ,
,
故直线 的方程为
的方程为 ,即
,即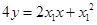 ,
,
所以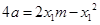 ,同理可得:
,同理可得: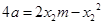
借助于根与系数的关系得到即 ,
,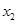 是方程
是方程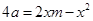 的两个不同的根,所以
的两个不同的根,所以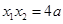
由已知易得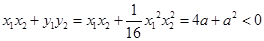 ,即
,即
解:(Ⅰ)由已知易得双曲线焦距为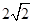 ,离心率为
,离心率为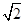 ,则长轴长为2,故双曲线的上顶点为
,则长轴长为2,故双曲线的上顶点为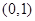 ,所以抛物线
,所以抛物线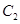 的方程
的方程
(Ⅱ)设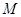 为
为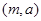 ,
,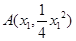 ,
, ,
,
故直线 的方程为
的方程为 ,即
,即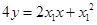 ,
,
所以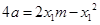 ,同理可得:
,同理可得: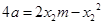 ,
,
即 ,
,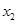 是方程
是方程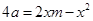 的两个不同的根,所以
的两个不同的根,所以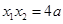
由已知易得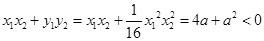 ,即
,即
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com