
题目列表(包括答案和解析)
 如图,有三个生活小区(均可看成点)分别位于A、B、C三点处,AB=AC,A到线段BC的距离AO=40,∠ABO=
如图,有三个生活小区(均可看成点)分别位于A、B、C三点处,AB=AC,A到线段BC的距离AO=40,∠ABO=| 2π |
| 7 |
| 2π |
| 7 |
2
| ||
| 3 |
| 2π |
| 7 |
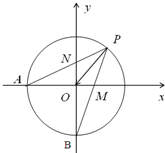 如图,点P是单位圆在第一象限上的任意一点,点A(-1,0),点B(0,-1),PA与y轴于点N,PB与x轴交于点M,设
如图,点P是单位圆在第一象限上的任意一点,点A(-1,0),点B(0,-1),PA与y轴于点N,PB与x轴交于点M,设| PO |
| PM |
| PN |
 (2013•安庆三模)如图,倾斜角为θ的直线OP与单位圆在第一象限的部分交于点P,单位圆与坐标轴交于点A(-1,0),点B(0,-1),PA与y轴交于点N,PB与x轴交于点M,设
(2013•安庆三模)如图,倾斜角为θ的直线OP与单位圆在第一象限的部分交于点P,单位圆与坐标轴交于点A(-1,0),点B(0,-1),PA与y轴交于点N,PB与x轴交于点M,设| PO |
| PM |
| PN |
 如图所示,一隧道内设双行线公路,其截面由长方形的三条边和抛物线的一段构成,为保证安全,要求行驶车辆顶部(设为平顶)与隧道顶部在竖直方向上高度之差至少要有0.5米.
如图所示,一隧道内设双行线公路,其截面由长方形的三条边和抛物线的一段构成,为保证安全,要求行驶车辆顶部(设为平顶)与隧道顶部在竖直方向上高度之差至少要有0.5米. 19、如图,一隧道内设双行线公路,其截面由一个长方形和抛物线构成,为保安全,要求行驶车辆顶部(设为平顶)与隧道顶部在竖直方向上高度之差至少要有0.5m.若行驶车道总宽度AB为6m,计算车辆通过隧道的限制高度是多少米?(精确到0.1m)
19、如图,一隧道内设双行线公路,其截面由一个长方形和抛物线构成,为保安全,要求行驶车辆顶部(设为平顶)与隧道顶部在竖直方向上高度之差至少要有0.5m.若行驶车道总宽度AB为6m,计算车辆通过隧道的限制高度是多少米?(精确到0.1m)湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com