
题目列表(包括答案和解析)
X1 | 5% | 10% |
|
| X2 | 2% | 8% | 12% |
P | 0.8 | 0.2 |
|
| P | 0.2 | 0.5 | 0.3 |
(1)在A、B两个项目上各投资100万元,Y1和Y2分别表示投资项目A和B所获得的利润,求方差DY1、DY2;(2)将x(0≤x≤100)万元投资A项目,100-x万元投资B项目,f(x)表示投资A项目所得利润的方差与投资B项目所得利润的方差的和。求f(x)的最小值,并指出x为何值时,f(x)取到最小值。 (注:D(aX + b) = a2DX)
| X1 | 5% | 10% |
| P | 0.8 | 0.2 |
| X2 | 2% | 8% | 12% |
| P | 0.2 | 0.5 | 0.3 |
为调查深圳市中学生平均每人每天参加体育锻炼时间X(单位:分钟),按锻炼时间分下列4种情况统计:(1)0-10分钟;(2)11-20分钟;(3)21-30分钟;(4)30分钟以上.有10000名中学生参加了此项调查活动,下图是此次调查中某一项的流程图,其输出的结果是6200,则平均每天参加体育锻炼时间在0-20分钟的学生的频率是

A.3800
B.6200
C.0.38
D.0.62
为调查某社区居民的业余生活状况,研究这一社区居民在20:00-22:00时间段的休闲方式与性别的关系,随机调查了该社区80人,得到下面的数据表:
| 休闲方式 性别 | 看电视 | 看书 | 合计 |
| 男 | 10 | 50 | 60 |
| 女 | 10 | 10 | 20 |
| 合计 | 20 | 60 | 80 |
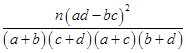 ,其中n=a+b+c+d.
,其中n=a+b+c+d.| P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
下列命题正确的是( )
A.若p q为假,则p,q均为假命题;
q为假,则p,q均为假命题;
B.“x 2”是“x2-3x+2
2”是“x2-3x+2 0”的充分不必要条件;
0”的充分不必要条件;
C.对命题p: x
x R,使得x2+x+1
R,使得x2+x+1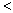 0,则
0,则 p为
p为 x
x R,均有x2+x+1
R,均有x2+x+1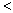 0;
0;
D.命题“若x2-3x+2=0,则x=1”的逆否命题为“若x=1,则x2-3x+2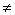 0”.
0”.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com