14．对数函数问题时.你注意到真数与底数的限制条件了吗?(真数大于零.底数大于零且不等于1)字母底数还需讨论呀. 【查看更多】

题目列表(包括答案和解析)

（理科做）
阅读下面题目的解法，再根据要求解决后面的问题．
阅读题目：对于任意实数a₁，a₂，b₁，b₂，证明不等式（a₁b₁+a₂b₂）²≤（a₁²+a₂²）（b₁²+b₂²）．
证明：构造函数f（x）=（a₁x+b₁）²+（a₂x+b₂）²=（a₁²+a₂²）x²+2（a₁b₁+a₂b₂）x+（b₁²+b₂²）．
注意到f（x）≥0，所以△=[2（a₁b₁+a₂b₂）]²-4（a₁²+a₂²）（b₁²+b₂²）≤0，
即（a₁b₁+a₂b₂）²≤（a₁²+a₂²）（b₁²+b₂²）．
（其中等号成立当且仅当a₁x+b₁=a₂x+b₂=0，即a₁b₂=a₂b₁．）
问题：（1）请用这个不等式证明：对任意正实数a，b，x，y，不等式

≥

(a+b)2

x+y

成立．
（2）用（1）中的不等式求函数y=

1-2x

(0＜x＜

)的最小值，并指出此时x的值．
（3）根据阅读题目的证明，将不等式（a₁b₁+a₂b₂）²≤（a₁²+a₂²）（b₁²+b₂²）进行推广，得到一个更一般的不等式，并用构造函数的方法对你的推广进行证明．

查看答案和解析>>

“实系数一元二次方程ax²+bx+c=0有实数解”转化为“△=b²-4ac≥0”，你是否注意到必须a≠0；当a=0时，“方程有解”不能转化为△=b²-4ac≥0．若原题中没有指出是“二次”方程、函数或不等式，你是否考虑到二次项系数可能为零的情形？

查看答案和解析>>

人口的增长是当前世界上各国普遍关注的问题.我们经常在报刊上看到关于人口增长的预报,说到本世纪中叶,全世界(或某地区)人口将达到多少亿.你可能注意到不同的报刊对同一时间的人口预报在数字上有较大的区别.你知道他们是如何预测的吗?为什么会有较大的区别呢?

早在1798年,英国经济学家马尔萨斯就提出自然状态下的人口增长模型y=y₀·e^rt,其中t表示时间,y₀表示t=0时的人口数,r表示人口的年平均增长率.

下面两个表格是我国两段时期的人口资料,试分别求出这两段时期的人口模型,并进行比较,解释为什么会不同,并预测2010年时我国人口总数.

甲 1950—1959

年份	1950	1951	1952	1953	1954
人数(万)	55 196	56 300	57 482	58 796	60 266
年份	1955	1956	1957	1958	1959
人数(万)	61 456	62 828	64 563	65 994	67 207

乙 1991—1998

年份	1991	1992	1993	1994
人数(万)	114 333	115 823	117 171	118 517
年份	1995	1996	1997	1998
人数(万)	119 850	121 121	122 389	123 626

查看答案和解析>>

（理科做）
阅读下面题目的解法，再根据要求解决后面的问题．
阅读题目：对于任意实数a₁，a₂，b₁，b₂，证明不等式（a₁b₁+a₂b₂）²≤（a₁²+a₂²）（b₁²+b₂²）．
证明：构造函数f（x）=（a₁x+b₁）²+（a₂x+b₂）²=（a₁²+a₂²）x²+2（a₁b₁+a₂b₂）x+（b₁²+b₂²）．
注意到f（x）≥0，所以△=[2（a₁b₁+a₂b₂）]²-4（a₁²+a₂²）（b₁²+b₂²）≤0，
即（a₁b₁+a₂b₂）²≤（a₁²+a₂²）（b₁²+b₂²）．
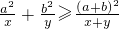（其中等号成立当且仅当a₁x+b₁=a₂x+b₂=0，即a₁b₂=a₂b₁．）
问题：（1）请用这个不等式证明：对任意正实数a，b，x，y，不等式 $数学公式$ 成立．
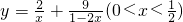（2）用（1）中的不等式求函数 $数学公式$ 的最小值，并指出此时x的值．
（3）根据阅读题目的证明，将不等式（a₁b₁+a₂b₂）²≤（a₁²+a₂²）（b₁²+b₂²）进行推广，得到一个更一般的不等式，并用构造函数的方法对你的推广进行证明．

查看答案和解析>>

已知集合

（I）证明：；

（II）某同学注意到是周期函数，也是偶函数，于是他着手探究：M中的元素是否都是周期函数？是否都是偶函数？对这两个问题，给出并证明你的结论.

查看答案和解析>>

同步练习册答案

练习册

高中

初中

小学