
题目列表(包括答案和解析)
早在1798年,英国经济学家马尔萨斯就提出自然状态下的人口增长模型y=y0·ert,其中t表示时间,y0表示t=0时的人口数,r表示人口的年平均增长率.
下面两个表格是我国两段时期的人口资料,试分别求出这两段时期的人口模型,并进行比较,解释为什么会不同,并预测2010年时我国人口总数.
甲 1950—1959
年份 | 1950 | 1951 | 1952 | 1953 | 1954 |
人数(万) | 55 196 | 56 300 | 57 482 | 58 796 | 60 266 |
年份 | 1955 | 1956 | 1957 | 1958 | 1959 |
人数(万) | 61 456 | 62 828 | 64 563 | 65 994 | 67 207 |
乙 1991—1998
年份 | 1991 | 1992 | 1993 | 1994 |
人数(万) | 114 333 | 115 823 | 117 171 | 118 517 |
年份 | 1995 | 1996 | 1997 | 1998 |
人数(万) | 119 850 | 121 121 | 122 389 | 123 626 |
(本题满分18分) 本题共有3个小题,第1小题满分4分,第2小题满分6分. 第3小题满分8分.
(文)对于数列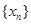 ,从中选取若干项,不改变它们在原来数列中的先后次序,得到的数列称为是原来数列的一个子数列. 某同学在学习了这一个概念之后,打算研究首项为
,从中选取若干项,不改变它们在原来数列中的先后次序,得到的数列称为是原来数列的一个子数列. 某同学在学习了这一个概念之后,打算研究首项为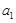 ,公差为
,公差为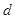 的无穷等差数列
的无穷等差数列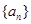 的子数列问题,为此,他取了其中第一项
的子数列问题,为此,他取了其中第一项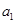 ,第三项
,第三项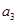 和第五项
和第五项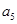 .
.
(1) 若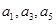 成等比数列,求
成等比数列,求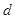 的值;
的值;
(2) 在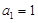 ,
, 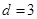 的无穷等差数列
的无穷等差数列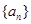 中,是否存在无穷子数列
中,是否存在无穷子数列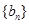 ,使得数列
,使得数列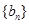 为等比数列?若存在,请给出数列
为等比数列?若存在,请给出数列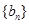 的通项公式并证明;若不存在,说明理由;
的通项公式并证明;若不存在,说明理由;
(3) 他在研究过程中猜想了一个命题:“对于首项为正整数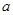 ,公比为正整数
,公比为正整数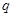 (
(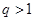 )的无穷等比数 列
)的无穷等比数 列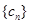 ,总可以找到一个子数列
,总可以找到一个子数列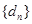 ,使得
,使得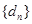 构成等差数列”. 于是,他在数列
构成等差数列”. 于是,他在数列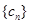 中任取三项
中任取三项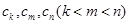 ,由
,由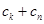 与
与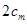 的大小关系去判断该命题是否正确. 他将得到什么结论?
的大小关系去判断该命题是否正确. 他将得到什么结论?
(本题满分18分) 本题共有3个小题,第1小题满分4分,第2小题满分6分. 第3小题满分8分.
(文)对于数列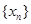 ,从中选取若干项,不改变它们在原来数列中的先后次序,得到的数列称为是原来数列的一个子数列. 某同学在学习了这一个概念之后,打算研究首项为
,从中选取若干项,不改变它们在原来数列中的先后次序,得到的数列称为是原来数列的一个子数列. 某同学在学习了这一个概念之后,打算研究首项为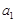 ,公差为
,公差为 的无穷等差数列
的无穷等差数列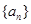 的子数列问题,为此,他取了其中第一项
的子数列问题,为此,他取了其中第一项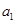 ,第三项
,第三项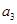 和第五项
和第五项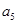 .
.
(1) 若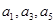 成等比数列,求
成等比数列,求 的值;
的值;
(2) 在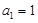 ,
, 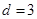 的无穷等差数列
的无穷等差数列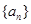 中,是否存在无穷子数列
中,是否存在无穷子数列 ,使得数列
,使得数列 为等比数列?若存在,请给出数列
为等比数列?若存在,请给出数列 的通项公式并证明;若不存在,说明理由;
的通项公式并证明;若不存在,说明理由;
(3) 他在研究过程中猜想了一个命题:“对于首项为正整数 ,公比为正整数
,公比为正整数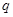 (
( )的无穷等比数 列
)的无穷等比数 列 ,总可以找到一个子数列
,总可以找到一个子数列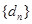 ,使得
,使得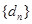 构成等差数列”. 于是,他在数列
构成等差数列”. 于是,他在数列 中任取三项
中任取三项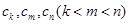 ,由
,由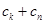 与
与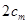 的大小关系去判断该命题是否正确. 他将得到什么结论?
的大小关系去判断该命题是否正确. 他将得到什么结论?
(1)类比“等差数列”给出“等和数列”的定义.
(2)探索等和数列{an}的奇数项与偶数项各有什么特点,并加以说明.
(3)在等和数列{an}中,如果a1=a,a2=b,求它的前n项和Sn.?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com