1．    (本小题满分12分)

如图，在四棱锥P—ABCD中，底面ABCD是矩形，已知AB = 3，AD = 2，PA = 2，，．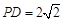

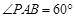(1)    证明：AD⊥平面PAB；

(2)    求异面直线PC与AD所成的角的大小；

(3)    求二面角P—BD—A的大小．

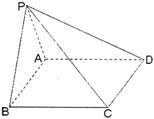
1．    (本小题满分12分)

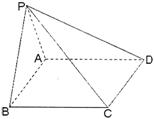
如图，在四棱锥P—ABCD中，底面ABCD是矩形，已知AB = 3，AD = 2，PA = 2，，．

(1)    证明：AD⊥平面PAB；

(2)    求异面直线PC与AD所成的角的大小；

(3)    求二面角P—BD—A的大小．

（本小题满分12分）

       某建筑工地在一块长AM=30米，宽AN=20米的矩形地块AMPN上施工，规划建设占地如图中矩形ABCD的学生公寓，要求顶点C在地块的对角线MN上，B，D分别在边AM，AN上，假设AB长度为米。

   （Ⅰ）要使矩形学生公寓ABCD的面积不小于144平方米，AB的长度应在什么范围？

   （Ⅱ）长度AB和宽度AD分别为多少米时矩形学生公寓ABCD的面积最大？最大值是多少平方米？

（本小题满分12分）如图，已知正方形ABCD和矩形ACEF所在平面互相垂直，
AB=，AF=1，M是线段EF的中点。
(Ⅰ)求证：AM∥平面BDE；
(Ⅱ) 求二面角A－DF－B的大小.
（Ⅲ）试问：在线段AC上是否存在一点P，使得直线PF与AD所成角为60°？