
题目列表(包括答案和解析)
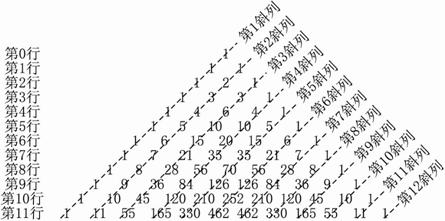
试回答:(其中第(1)&(5)小题只需直接给出最后的结果,无需求解过程)
(1)记第i(i∈N*)行中从左到右的第j(j∈N*)个数为aij,则数列{aij}的通项公式为 ,
n阶杨辉三角中共有 个数;
(2)第k行各数的和是;
(3)n阶杨辉三角的所有数的和是;
(4)将第n行的所有数按从左到右的顺序合并在一起得到的多位数等于;
(5)第p(p∈N*,且p≥2)行除去两端的数字1以外的所有数都能被p整除,则整数p一定为( )
A.奇数 B.质数 C.非偶数 D.合数
(6)在第3斜列中,前5个数依次为1、3、6、10、15;第4斜列中,第5个数为35.显然,1+3+6+10+15=35.事实上,一般地有这样的结论:
第m斜列中(从右上到左下)前k个数之和,一定等于第m+1斜列中第k个数.
试用含有m、k(m、k∈N*)的数学公式表示上述结论并证明其正确性.
数学公式为 .
证明: .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com