
题目列表(包括答案和解析)
8. 点![]() 在直线
在直线![]() :
:![]() 上,若存在过
上,若存在过![]() 的直线交抛物线
的直线交抛物线![]() 于
于![]() ,
,![]() 两点,且
两点,且![]() ,则称点
,则称点![]() 为“
为“![]() 点”,那么下列结论中正确的是
点”,那么下列结论中正确的是
A.直线![]() 上的所有点都是“
上的所有点都是“![]() 点” B.直线
点” B.直线![]() 上仅有有限个点是“
上仅有有限个点是“![]() 点”
点”
C.直线![]() 上的所有点都不是“
上的所有点都不是“![]() 点” D.直线
点” D.直线![]() 上有无穷多个点(点不是所有的点)是“
上有无穷多个点(点不是所有的点)是“![]() 点”
点”
直线 与抛物线
与抛物线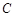 :
: 交于
交于 两点,点
两点,点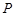 是抛物线
是抛物线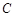 准线上的一点,
准线上的一点,
记 ,其中
,其中 为抛物线
为抛物线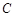 的顶点.
的顶点.
(1)当 与
与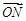 平行时,
平行时, ________;
________;
(2)给出下列命题:
① ,
, 不是等边三角形;
不是等边三角形;
②
 且
且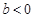 ,使得
,使得 与
与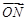 垂直;
垂直;
③无论点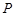 在准线上如何运动,
在准线上如何运动,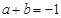 总成立.
总成立.
其中,所有正确命题的序号是___.
直线
 与椭圆
与椭圆 相交于
相交于 ,
,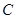 两点,
两点,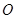 为坐标原点.
为坐标原点.
(Ⅰ)当点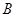 的坐标为
的坐标为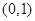 ,且四边形
,且四边形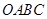 为菱形时,求
为菱形时,求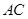 的长;
的长;
(Ⅱ)当点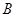 在
在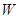 上且不是
上且不是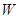 的顶点时,证明:四边形
的顶点时,证明:四边形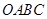 不可能为菱形.
不可能为菱形.
直线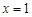 与抛物线
与抛物线 :
: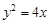 交于
交于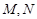 两点,点
两点,点 是抛物线
是抛物线 准线上的一点,
准线上的一点,
记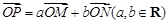 ,其中
,其中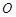 为抛物线
为抛物线 的顶点.
的顶点.
(1)当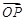 与
与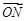 平行时,
平行时,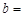 ________;
________;
(2)给出下列命题:
①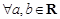 ,
,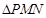 不是等边三角形;
不是等边三角形;
②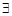
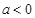 且
且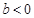 ,使得
,使得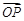 与
与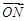 垂直;
垂直;
③无论点 在准线上如何运动,
在准线上如何运动,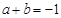 总成立.
总成立.
其中,所有正确命题的序号是___.
直线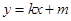
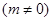 与椭圆
与椭圆 相交于
相交于 ,
,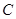 两点,
两点, 为坐标原点.
为坐标原点.
(Ⅰ)当点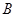 的坐标为
的坐标为 ,且四边形
,且四边形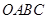 为菱形时,求
为菱形时,求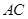 的长;
的长;
(Ⅱ)当点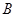 在
在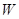 上且不是
上且不是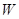 的顶点时,证明:四边形
的顶点时,证明:四边形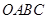 不可能为菱形.
不可能为菱形.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com