
题目列表(包括答案和解析)
| 1 | 2 |
若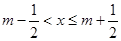 (其中
(其中 为整数),则称
为整数),则称 为离实数
为离实数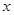 最近的整数,记作
最近的整数,记作 ,即
,即 .设集合
.设集合 ,
, ,若集合
,若集合 的子集恰有两个,则
的子集恰有两个,则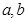 的取值不可能是( )
的取值不可能是( )
A. | B.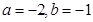 |
C. | D. |
若 (其中
(其中 为整数),则称
为整数),则称 为离实数
为离实数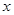 最近的整数,记作
最近的整数,记作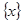 ,即
,即 .设集合
.设集合 ,
, ,若集合
,若集合 的子集恰有两个,则
的子集恰有两个,则 的取值不可能是(
)
的取值不可能是(
)
A. B.
B.
C. D.
D.
已知集合“◆”的元素是在以四点(-2,0)、(1,-3)、(4,0)、(1,3)为顶点的正方形内部,并且坐标都是整数的“整点”.定义在集合“◆”的元素中,两个坐标之和为偶数的点称为“偶点”,由“偶点”构成的集合称为“偶点集”,记作“■”,那么集合“■”的补集,即“![]() ◆■”中所有元素的个数为 ( )
◆■”中所有元素的个数为 ( )
A.8 B.9 C.11 D.13
 (其中
(其中 为整数),则称
为整数),则称 为离实数
为离实数 最近的整数,记作
最近的整数,记作 ,即
,即 .设集合
.设集合 ,
, ,若集合
,若集合 的子集恰有两个,则
的子集恰有两个,则 的取值不可能是( )
的取值不可能是( )A. | B. |
C. | D. |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com