
题目列表(包括答案和解析)
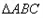 中,角
中,角 的对边分别为
的对边分别为 ,且
,且
 ;
; 将函数
将函数 的图象上各点的纵坐标保持不变,横坐标缩短到原来的
的图象上各点的纵坐标保持不变,横坐标缩短到原来的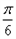 ,把所得图象向右平移
,把所得图象向右平移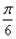 个单位,得到函数
个单位,得到函数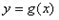 的图象,求函数
的图象,求函数 的对称中心及单调递增区间.
的对称中心及单调递增区间. 已知函数![]() 图象的对称中心为(0,1);函数
图象的对称中心为(0,1);函数![]() 在 区间[-2,1)上单调递减,在[1, +∞)上单调递增.
在 区间[-2,1)上单调递减,在[1, +∞)上单调递增.
(Ⅰ)求实数b的值;
(Ⅱ)求![]() 的值及
的值及![]() 的解析式;
的解析式;
(Ⅲ)设![]() ,试证:对任意的x1、x2∈(1,+∞)且x1≠x2,都有
,试证:对任意的x1、x2∈(1,+∞)且x1≠x2,都有
![]() .
.
下图展示了一个区间(0,k)(k是一个给定的正实数)到实数集R的对应过程:区间(0,k)中的实数m对应线段AB上的点M,如图1;将线段AB弯成半圆弧,圆心为H,如图2;再将这个半圆置于直角坐标系中,使得圆心H坐标为(0,1),直径AB平行x轴,如图3;在图形变化过程中,图1中线段AM的长度对应于图3中的圆弧AM的长度,直线HM与直线y=-1相交与点N(n,-1),则与实数m对应的实数就是n,记作n=f(m).给出下列命题:
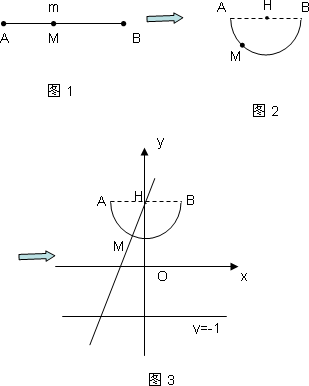
(1)![]() ;
;
(2)函数n=f(m)是奇函数;
(3)n=f(m)是定义域上的单调递增函数;
(4)n=f(m)的图象关于点![]() 对称;
对称;
(5)方程f(m)=2的解是![]() .
.
其中正确命题序号为________.
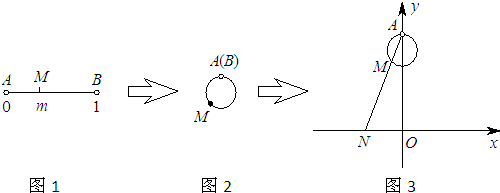
下图展示了一个区间(0,k)(k是一个给定的正实数)到实数集R的对应过程:区间(0,k)中的实数m对应线段AB上的点M,如图1;将线段AB弯成半圆弧,圆心为H,如图2;再将这个半圆置于直角坐标系中,使得圆心H坐标为(0,1),直径AB平行x轴,如图3;在图形变化过程中,图1中线段AM的长度对应于图3中的圆弧AM的长度,直线HM与直线y=-1相交与点N(n,-1),则与实数m对应的实数就是n,记作n=f(m).给出下列命题:

(1)![]() ;(2)函数n=f(m)是奇函数;(3)n=f(m)是定义域上的单调递增函数;(4)n=f(m)的图象关于点
;(2)函数n=f(m)是奇函数;(3)n=f(m)是定义域上的单调递增函数;(4)n=f(m)的图象关于点![]() 对称;(5)方程f(m)=2的解是
对称;(5)方程f(m)=2的解是![]() .
.
其中正确命题序号为________.
| 1 |
| 2 |
| 1 |
| 2 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com