
题目列表(包括答案和解析)
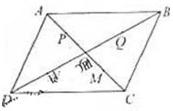 在平行四边形ABCD中,O是AC与BD的交点,P、Q、M、N分别是线段OA、OB、OC、OD的中点,在APMC中任取一点记为E,在B、Q、N、D中任取一点记为F,设G为满足向量
在平行四边形ABCD中,O是AC与BD的交点,P、Q、M、N分别是线段OA、OB、OC、OD的中点,在APMC中任取一点记为E,在B、Q、N、D中任取一点记为F,设G为满足向量| OG |
| OE |
| OF |
在平行四边形ABCD中,O是AC与BD的交点,P、Q、M、N分别是线段OA、OB、OC、OD的中点,在APMC中任取一点记为E,在B、Q、N、D中任取一点记为F,设G为满足向量![]() 的点,则在上述的点G组成的集合中的点,落在平行四边形ABCD外(不含边界)的概率为 。
的点,则在上述的点G组成的集合中的点,落在平行四边形ABCD外(不含边界)的概率为 。

在平行四边形ABCD中,O是AC与BD的交点,P、Q、M、N分别是线段OA、OB、OC、OD的中点,在APMC中任取一点记为E,在B、Q、N、D中任取一点记为F,设G为满足向量![]() 的点,则在上述的点G组成的集合中的点,落在平行四边形ABCD外(不含边界)的概率为 。
的点,则在上述的点G组成的集合中的点,落在平行四边形ABCD外(不含边界)的概率为 。
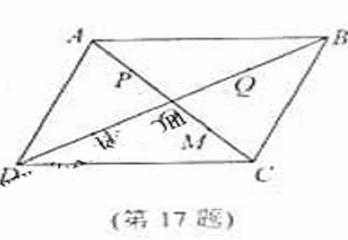
 的点,则在上述的点G组成的集合中的点,落在平行四边形ABCD外(不含边界)的概率为 .
的点,则在上述的点G组成的集合中的点,落在平行四边形ABCD外(不含边界)的概率为 .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com