
题目列表(包括答案和解析)
|
| 组数 | 分组 | 頻数 | 频率 | 光盘族占本组的比例 |
| 第一组 | [25,30﹚ | 50 | 0.05 | 30% |
| 第二组 | [30,35﹚ | 100 | 0.1 | 30% |
| 第三组 | [35,40﹚ | 150 | 0.15 | 40% |
| 第四组 | [40,45﹚ | 200 | 0.2 | 50% |
| 第五组 | [45,50﹚ | a | b | 65% |
| 第六组 | [50,55﹚ | 200 | 0.2 | 60% |
(本小题满分12分)
班主任为了对本班学生的考试成绩进行分析,决定从全班25位女同学,15位男同学中随机抽取一个容量为8的样本进行分析.
(1)如果按性别比例分层抽样,则样本中男、女生各有多少人;
(2)随机抽取8位同学,数学分数依次为:60,65,70,75,80,85,90,95;
物理成绩依次为:72,77,80,84,88,90,93,95,
①若规定80分(含80分)以上为良好,90分(含90分)以上为优秀,在良好的条件下,求两科均为优秀的概率;
②若这8位同学的数学、物理分数事实上对应下表:
|
学生编号 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
数学分数 |
60 |
65 |
70 |
75 |
80 |
85 |
90 |
95[来源:Z&xx&k.Com] |
|
物理分数 |
72 |
77 |
80 |
84 |
88 |
90 |
93 |
95 |
根据上表数据可知,变量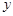 与
与 之间具有较强的线性相关关系,求出
之间具有较强的线性相关关系,求出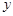 与
与 的线性回归方程(系数精确到0.01).(参考公式:
的线性回归方程(系数精确到0.01).(参考公式: ,其中
,其中 ,
, ;参考数据:
;参考数据: ,
,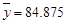 ,
, ,
,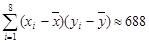 ,
, ,
, ,
,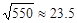 )
)
(本小题12分)
射手张强在一次 射击中射中10环、9环、8环、7环、7环以下的概率分别是0.24,0.28,0.19,0.16,0.13.计算这个射手在一次射击中:
射击中射中10环、9环、8环、7环、7环以下的概率分别是0.24,0.28,0.19,0.16,0.13.计算这个射手在一次射击中:
(1)射中10环或9环的概率;
(2)至少射中7环的概率;
(3)射中环数不足8环的概率.

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com