
题目列表(包括答案和解析)
(本小题满分14分,第Ⅰ小题5分,第Ⅱ小题4分,第Ⅲ小题5分).
数列![]() 的各项均为正数,
的各项均为正数,![]() 为其前
为其前![]() 项和,对于任意
项和,对于任意![]() ,总有
,总有![]() 成等差数列.
成等差数列.
(Ⅰ)求数列![]() 的通项公式;
的通项公式;
(Ⅱ)设数列![]() 的前
的前![]() 项和为
项和为![]() ,且
,且![]() ,求证:对任意实数
,求证:对任意实数![]() (
(![]() 是常数,
是常数,![]() =2.71828
=2.71828![]() )和任意正整数
)和任意正整数![]() ,总有
,总有![]()
![]() 2;
2;
(Ⅲ) 正数数列![]() 中,
中,![]() .求数列
.求数列![]() 中的最大项.
中的最大项.
 (本小题满分14分)设b>0,椭圆方程为
(本小题满分14分)设b>0,椭圆方程为![]() ,抛物线方程为
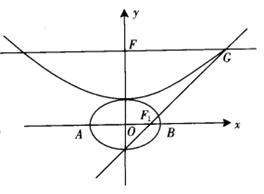
,抛物线方程为![]() .如图4所示,过点F(0,b+2)作x轴的平行线,与抛物线在
.如图4所示,过点F(0,b+2)作x轴的平行线,与抛物线在
第一象限的交点为G.已知抛物线在点G的切线经
过椭圆的右焦点![]() .
.
(1)求满足条件的椭圆方程和抛物线方程;
(2)设A,B分别是椭圆长轴的左、右端点,试探究在
抛物线上是否存在点P,使得△ABP为直角三角形?
若存在,请指出共有几个这样的点?并说明理由
(不必具体求出这些点的坐标).
(本小题满分14分)设数列{an}为前n项和为Sn,数列{bn}满足:bn =nan,且数列{bn}的前n项和为(n-1)Sn+2n (n∈N*).
(1)求a1,a2的值;
(2)求证:数列{ Sn +2}是等比数列;
(3)抽去数列{an}中的第1项,第4项,第7项,……,第3n-2项,余下的项顺序不变,组成一个新数列{cn},若{cn}的前n项和为Tn,求证:
<≤
(本小题满分14分)
在一次数学考试中,第21题和第22题为选做题,规定每位考生必须且只须在其中选做一题.设每位考生选做每一题的可能性均为![]() .
.
(1)求甲、乙两名学生选做同一道题的概率;
(2)设4名考生中选做第22题的学生个数为![]() ,求
,求![]() 的概率分布及数学期望.
的概率分布及数学期望.
(本小题满分14分)
某市一家庭今年一月份、二月份和三月份煤气用量和支付费用如下表所示:
|
月份 |
用气量(立方米) |
煤气费(元) |
|
1 |
4 |
4.00 |
|
2 |
25 |
14.00 |
|
3 |
35 |
19.00 |
该市煤气收费的方法是:煤气费=基本费十超额费十保险费.
若每月用气量不超过最低额度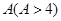 立方米时,只付基本费
立方米时,只付基本费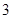 元和每户每月定额保险费
元和每户每月定额保险费 元;若用气量超过
元;若用气量超过 立方米时,超过部分每立方米付
立方米时,超过部分每立方米付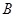 元.
元.
(1)根据上面的表格求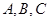 的值;
的值;
(2)记用户第四月份用气为 立方米,求他应交的煤气费
立方米,求他应交的煤气费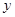 (元).
(元).
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com