
题目列表(包括答案和解析)
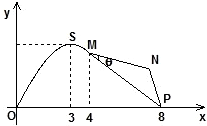 如图,某市拟在长为8km的道路OP的一侧修建一条运动赛道,赛道的前一部分为曲线段OSM,该曲线段为函数y=Asinωx(A>0,ω>0)x∈[0,4]的图象,且图象的最高点为S(3,2
如图,某市拟在长为8km的道路OP的一侧修建一条运动赛道,赛道的前一部分为曲线段OSM,该曲线段为函数y=Asinωx(A>0,ω>0)x∈[0,4]的图象,且图象的最高点为S(3,2| 3 |
如图,某市拟在长为8km的道路OP的一侧修建一条运动赛道,赛道的前一部分为曲线段OSM,该曲线段为函数y=Asin![]() x(A>0,
x(A>0, ![]() >0) x
>0) x![]() [0,4]的图象,且图象的最高点为
[0,4]的图象,且图象的最高点为
S(3,2![]() );赛道的后一部分为折线段MNP,为保证参赛运动员的安全,限定
);赛道的后一部分为折线段MNP,为保证参赛运动员的安全,限定![]() MNP=120
MNP=120![]()
(I)求A , ![]() 的值和M,P两点间的距离;
的值和M,P两点间的距离;
(II)应如何设计,才能使折线段赛道MNP最长?
 w.w.w.k.s.5.u.c.o.m
w.w.w.k.s.5.u.c.o.m ![]()
![]()
如图,某市拟在长为8km的道路OP的一侧修建一条运动赛道,赛道的前一部分为曲线段OSM,该曲线段为函数y=Asin![]() x(A>0,
x(A>0, ![]() >0) x
>0) x![]() [0,4]的图象,且图象的最高点为
[0,4]的图象,且图象的最高点为
S(3,2![]() );赛道的后一部分为折线段MNP,为保证参赛运动员的安全,限定
);赛道的后一部分为折线段MNP,为保证参赛运动员的安全,限定![]() MNP=120
MNP=120![]()
(I)求A , ![]() 的值和M,P两点间的距离;
的值和M,P两点间的距离;
(II)应如何设计,才能使折线段赛道MNP最长?

 如图,某市拟在长为8km的道路OP的一侧修建一条运动赛道,赛道的前一部分为曲线段OSM,该曲线段为函数y=Asinωx(A>0,ω>0)x∈[0,4]的图象,且图象的最高点为
如图,某市拟在长为8km的道路OP的一侧修建一条运动赛道,赛道的前一部分为曲线段OSM,该曲线段为函数y=Asinωx(A>0,ω>0)x∈[0,4]的图象,且图象的最高点为 ;赛道的后一部分为折线段MNP,为保证参赛运动员的安全,限定∠MNP=120°
;赛道的后一部分为折线段MNP,为保证参赛运动员的安全,限定∠MNP=120° 如图,某市拟在长为8km的道路OP的一侧修建一条运动赛道,赛道的前一部分为曲线段OSM,该曲线段为函数y=Asinωx(A>0,ω>0)x∈[0,4]的图象,且图象的最高点为
如图,某市拟在长为8km的道路OP的一侧修建一条运动赛道,赛道的前一部分为曲线段OSM,该曲线段为函数y=Asinωx(A>0,ω>0)x∈[0,4]的图象,且图象的最高点为 ;赛道的后一部分为折线段MNP,为保证参赛运动员的安全,限定∠MNP=120°
;赛道的后一部分为折线段MNP,为保证参赛运动员的安全,限定∠MNP=120°湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com