20．解:(1)当时.＝ ∴当时. -----------------------------------------------------------------2分当时.＝ ∵函数在上单——青夏教育精英家教网—

20．解:(1)当时.＝ ∴当时. -----------------------------------------------------------------2分当时.＝ ∵函数在上单调递增 ∴------------------------------4分由得又 ∴当时..当时..----------6分 (2)函数有零点即方程有解即有解-------------------------------------------------------------------------------7分令当时 ∵--------------------------------------------------------------------9分 ∴函数在上是增函数.∴---------------------------------------------10分当时. ∵--------------------------------12分 ∴函数在上是减函数.∴-----------------------------------------13分 ∴方程有解时即函数有零点时---------------------------------------------------------------------------14分【查看更多】

题目列表(包括答案和解析)

如图，这是解决某个问题而绘制的程序框图，仔细分析各图框内的内容及图框之间的关系，回答下列问题：

(1)该流程图解决的是怎样的一个问题？

(2)若最终输出的结果y₁＝3，y₂＝－2，当x取5时输出的结果5a＋b的值应该是多少？

(3)图框①中x＝2的含义是什么？

查看答案和解析>>

有时可用函数f(x)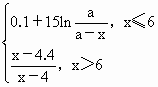＝描述学习某学科知识的掌握程度，其中x表示某学科知识的学习次数(x∈N₊)，f(x)表示对该学科知识的掌握程度，正实数a与学科知识有关．

(1)证明：当x≥7时，掌握程度的增加量f(x＋1)－f(x)总是下降；

(2)根据经验，学科甲、乙、丙对应的a的取值区间分别为(115，121]，(121，127]，(127，133]．当学习某学科知识6次时，掌握程度是85％，请确定相应的学科．

分析：根据已知条件作差，结合综合法可以确定作差所得的函数为减函数，从而得出结论；又根据函数模型代入数据可以解得参数a的近似值，通过对近似值所在区间加以判断并选择相应的学科．

查看答案和解析>>

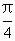已知：定义在区间[－，π]上的函数y＝f(x)的图像关于直线x＝对称，当x≥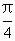时，函数f(x)＝sinx．

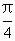(1)求f(－)，f(－)的值；

(2)求y＝f(x)的函数表达式(直接写表达式只得2分)；

(3)如果关于x的方程f(x)＝a有解，那么将方程在a取某一确定值时所求得的所有解的和记为M_a．求M_a的所有可能取值及相对应的a的取值范围．

查看答案和解析>>

通过研究学生的学习行为，专家发现，学生的注意力随老师讲课时间的变化而变化，讲课开始时，学生的兴趣激增；中间有一段时间，学生的兴趣保持较理想的状态，随后学生的注意力开始分散，设f(t)表示学生的注意力随时间t(分钟)的变化规律(注：f(t)越大，表明学生的注意力越集中)，经过实验分析得知：f(t)＝．