
题目列表(包括答案和解析)
如图,直线 与抛物线
与抛物线 交于
交于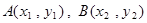 两点,与
两点,与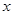 轴相交于点
轴相交于点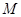 ,且
,且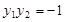 .
.
(1)求证: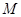 点的坐标为
点的坐标为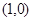 ;
;
(2)求证: ;
;
(3)求 的面积的最小值.
的面积的最小值.

【解析】设出点M的坐标 ,并把过点M的方程设出来.为避免对斜率不存在的情况进行讨论,可以设其方程为
,并把过点M的方程设出来.为避免对斜率不存在的情况进行讨论,可以设其方程为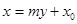 ,然后与抛物线方程联立消x,根据
,然后与抛物线方程联立消x,根据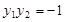 ,即可建立关于
,即可建立关于 的方程.求出
的方程.求出 的值.
的值.
(2)在第(1)问的基础上,证明: 即可.
即可.
(3)先建立面积S关于m的函数关系式,根据 建立即可,然后再考虑利用函数求最值的方法求最值.
建立即可,然后再考虑利用函数求最值的方法求最值.
已知过点 的动直线
的动直线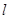 与抛物线
与抛物线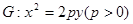 相交于
相交于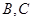 两点.当直线
两点.当直线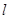 的斜率是
的斜率是 时,
时, .
.
(1)求抛物线 的方程;
的方程;
(2)设线段 的中垂线在
的中垂线在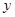 轴上的截距为
轴上的截距为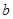 ,求
,求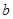 的取值范围.
的取值范围.
【解析】(1)B ,C
,C ,当直线
,当直线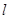 的斜率是
的斜率是 时,
时,
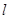 的方程为
的方程为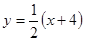 ,即
,即 (1’)
(1’)
联立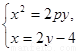 得
得 ,
,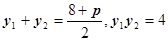 (3’)
(3’)
由已知  ,
,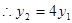 (4’)
(4’)
由韦达定理可得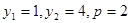 G方程为
G方程为 (5’)
(5’)
(2)设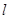 :
: ,BC中点坐标为
,BC中点坐标为 (6’)
(6’)
 得
得 由
由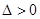 得
得 (8’)
(8’)

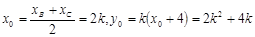
BC中垂线为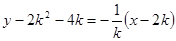 (10’)
(10’)

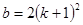 (11’)
(11’)

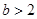
(本题满分12分)
直线![]() 过点P
过点P![]() (
(![]() 斜率为
斜率为![]() ,与直线
,与直线![]() :
:![]() 交于点A,与
交于点A,与![]() 轴交于点B,点A,B的横坐标分别为
轴交于点B,点A,B的横坐标分别为![]() ,记
,记![]() .
.
(Ⅰ)求![]() 的解析式;
的解析式;
(Ⅱ)设数列![]() 满足
满足![]() ,求数列
,求数列![]() 的通项公式;
的通项公式;
(Ⅲ)在(Ⅱ)的条件下,当![]() 时,证明不等式
时,证明不等式![]() .
.
(本题满分12分)
直线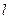 过点P
过点P (
( 斜率为
斜率为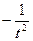 ,与直线
,与直线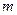 :
: 交于点A,与
交于点A,与 轴交于点B,点A,B的横坐标分别为
轴交于点B,点A,B的横坐标分别为 ,记
,记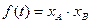 .
.
(Ⅰ)求 的解析式;
的解析式;
(Ⅱ)设数列 满足
满足 ,求数列
,求数列 的通项公式;
的通项公式;
(Ⅲ)在(Ⅱ)的条件下,当 时,证明不等式
时,证明不等式 .
.
(本题满分12分)
直线 过点P
过点P (
(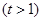 斜率为
斜率为 ,与直线
,与直线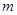 :
: 交于点A,与
交于点A,与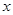 轴交于点B,点A,B的横坐标分别为
轴交于点B,点A,B的横坐标分别为 ,记
,记 .
.
(Ⅰ)求 的解析式;
的解析式;
(Ⅱ)设数列 满足
满足 ,求数列
,求数列 的通项公式;
的通项公式;
(Ⅲ)在(Ⅱ)的条件下,当 时,证明不等式
时,证明不等式 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com