练习册

  • 练习册
  • 试题
    如图.函数y=|x|在x∈［-1,1］的图象上有两点A.B.AB∥Ox轴.点 M(1.m), (m∈R且m >)是△ABC的BC边的中点 (1)写出用B点横坐标t表示△ABC面积S的函数解析式S=f(t); (2)求函数S=f(t)的最大值.并求出相应的C点坐标 【查看更多】

     

    题目列表(包括答案和解析)

    (本小题满分12分)已知函数f(x)=x2－1(x≥1)的图象是C1，函数y=g(x)的图象C2与C1关于直线y=x对称.
    (1)求函数y=g(x)的解析式及定义域M；
    (2)对于函数y=h(x)，如果存在一个正的常数a，使得定义域A内的任意两个不等的值x1，x2都有|h(x1)－h(x2)|≤a|x1－x2|成立，则称函数y=h(x)为A的利普希茨Ⅰ类函数.试证明：y=g(x)是M上的利普希茨Ⅰ类函数；
    (3)设A、B是曲线C2上任意不同两点，证明：直线AB与直线y=x必相交.

    查看答案和解析>>

    （本小题满分12分）

       围建一个面积为360m2的矩形场地，要求矩形场地的一面利用旧墙（利用旧墙需维修），其它三面围墙要新建，在旧墙的对面的新墙上要留一个宽度为2m的进出口，如图所示，已知旧墙的维修费用为45元/m，新墙的造价为180元/m，设利用的旧墙的长度为x（单位：元）。

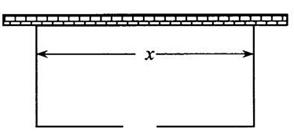
    （Ⅰ）将y表示为x的函数；

    （Ⅱ）试确定x，使修建此矩形场地围墙的总费用最小，并求出最小总费用。

    查看答案和解析>>

    .（本小题满分12分）在△ABC中，∠C = 90o ,BC = 1.以A为圆心，AC为半径画弧交AB于D，在由弧CD与直线段BD、BC所围成的范围内作内接正方形EFGH（如图）。设AC = x，EF = y ，（1）求y与x的函数关系式；（2）正方形EFGH的面积是否有最大值？试证明你的结论。

    查看答案和解析>>

    （本小题满分12分）
    如图：A、B两城相距100 km，某天燃气公司计划在两地之间建一天燃气站D 给A、B两城供气. 已知D地距A城x km，为保证城市安全，天燃气站距两城市的距离均不得少于10km . 已知建设费用y (万元)与A、B两地的供气距离(km)的平方和成正比，当天燃气站D距A城的距离为40km时, 建设费用为1300万元.（供气距离指天燃气站距到城市的距离）
    （1）把建设费用y(万元)表示成供气距离x (km)的函数，并求定义域；
    （2）天燃气供气站建在距A城多远，才能使建设供气费用最小.，最小费用是多少？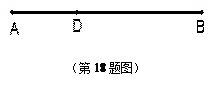

    查看答案和解析>>

    .（本小题满分12分）

    某地方政府准备在一块面积足够大的荒地上建一如图所示的一个矩形综合性休闲广场，其总面积为3000平方米，其中场地四周（阴影部分）为通道，通道宽度均为2米，中间的三个矩形区域将铺设塑胶地面作为运动场地（其中两个小场地形状相同），塑胶运动场地占地面积为S平方米.

    （1）   分别写出用x表示y和S的函数关系式（写出函数定义域）

    （2）   怎样设计能使s取得最大值，最大值为多少？

     

     

     

    查看答案和解析>>


    同步练习册答案