
题目列表(包括答案和解析)
关于不等式的性质:
①a>b![]() a+c>b+c;②a>b,b>c
a+c>b+c;②a>b,b>c![]() a>c;③a>b,c>0
a>c;③a>b,c>0![]() ac>bc;④a>b,c<0
ac>bc;④a>b,c<0![]() ac<bc;
ac<bc;
⑤a>b,c>d![]() a+c>b+d;⑥a>b>0,c>d>0
a+c>b+d;⑥a>b>0,c>d>0![]() ac>bd;⑦
ac>bd;⑦![]() ;
;
⑧![]() 。其中正确的有 (填序号)。
。其中正确的有 (填序号)。
关于不等式的性质:
①a>b![]() a+c>b+c;②a>b,b>c
a+c>b+c;②a>b,b>c![]() a>c;③a>b,c>0
a>c;③a>b,c>0![]() ac>bc;④a>b,c<0
ac>bc;④a>b,c<0![]() ac<bc;
ac<bc;
⑤a>b,c>d![]() a+c>b+d;⑥a>b>0,c>d>0
a+c>b+d;⑥a>b>0,c>d>0![]() ac>bd;⑦
ac>bd;⑦![]() ;
;
⑧![]() 。其中正确的有 (填序号)。
。其中正确的有 (填序号)。
| |||||
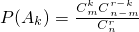 ,k=0,1,…,r.显然A0,A1,…,Ar为互斥事件,且A0∪A1∪…∪Ar=Ω(必然事件),因此1=P(Ω)=P(A0)+P(A1)+…P(Ar)=
,k=0,1,…,r.显然A0,A1,…,Ar为互斥事件,且A0∪A1∪…∪Ar=Ω(必然事件),因此1=P(Ω)=P(A0)+P(A1)+…P(Ar)=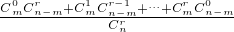 ,所以Cm0Cn-mr+Cm1Cn-mr-1+…+CmrCn-m0=Cnr,即等式(*)成立.对此,有的同学认为上述证明是正确的,体现了偶然性与必然性的统一;但有的同学对上述证明方法的科学性与严谨性提出质疑.现有以下四个判断:
,所以Cm0Cn-mr+Cm1Cn-mr-1+…+CmrCn-m0=Cnr,即等式(*)成立.对此,有的同学认为上述证明是正确的,体现了偶然性与必然性的统一;但有的同学对上述证明方法的科学性与严谨性提出质疑.现有以下四个判断:| 患心肺疾病 | 不患心肺疾病 | 合计 | |
| 男 | 20 | 5 | 25 |
| 女 | 10 | 15 | 25 |
| 合计 | 30 | 20 | 50 |
| P(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
| n(ad-bc)2 |
| (a+b)(c+d)(a+c)(b+d) |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com