练习册

  • 练习册
  • 试题
    8．设函数f(x)＝x|x|+bx+c.给出下列命题: ①b＝0.c>0时.方程f(x)＝0只有一个实数根, ②c＝0时.y＝f(x)是奇函数, ③方程f(x)＝0至多有两个实根． 上述三个命题中所有正确命题的序号为 ． 答案 ①② 解析 ①f(x)＝x|x|+c＝. 如图①.曲线与x轴只有一个交点. 所以方程f(x)＝0只有一个实数根.正确． ②c＝0时.f(x)＝x|x|+bx.显然是奇函数． ③当c＝0.b<0时. f(x)＝x|x|+bx＝. 如图②.方程f(x)＝0可以有三个实数根． 综上所述.正确命题的序号为①②. 【查看更多】

     

    题目列表(包括答案和解析)

    设函数f(θ)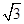＝sinθ＋cosθ，其中，角θ的顶点与坐标原点重合，始边与x轴非负半轴重合，终边经过点P(x，y)，且0≤θ≤π.
    (1)若点P的坐标为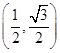，求f(θ)的值；
    (2)若点P(x，y)为平面区域Ω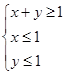：，上的一个动点，试确定角θ的取值范围，并求函数f(θ)的最小值和最大值．

    查看答案和解析>>

    设函数f(θ)＝sinθ＋cosθ，其中，角θ的顶点与坐标原点重合，始边与x轴非负半轴重合，终边经过点P(x，y)，且0≤θ≤π.

    (1)若点P的坐标为，求f(θ)的值；

    (2)若点P(x，y)为平面区域Ω：，上的一个动点，试确定角θ的取值范围，并求函数f(θ)的最小值和最大值．

     

    查看答案和解析>>

    如图，设A是单位圆和x轴正半轴的交点，P、Q是单位圆上的两点，O是坐标原点，∠AOP＝，∠AOQ＝α，α∈[0，π)．

    (1)若，求cos(α－)的值；

    (2)设函数f(α)＝·，求f(α)的值域．

    查看答案和解析>>

    解答题

    已知函数f(x)＝x2－1(x≥1)的曲线为C1，曲线C2与C1关于直线y＝x对称．

    (1)求曲线C2的方程y＝g(x)；

    (2)设函数y＝g(x)的定义域为M，x1，x2∈M，且x1≠x2，求证：|g(x1)－g(x2)|＜|x1－x2|：

    (3)设A、B为曲线C2上任意不同两点，证明直线AB与直线y＝x必相交．

    查看答案和解析>>

    已知函数f(x)＝－1(x≥1)的图象是，曲线与关于直线y＝x对称．

    (1)求曲线的方程y＝g(x)；

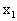    (2)设函数y＝g(x)的定义域为M，∈M，且，求证：|g()－g()|＜||；

    (3)设A，B是曲线上任意不同两点，证明直线AB与直线y＝x必相交．

    查看答案和解析>>


    同步练习册答案