
题目列表(包括答案和解析)
曲线y=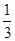 x3+
x3+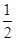 x2在点T(1,
x2在点T(1,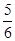 )处的切线与两坐标轴围成的三角形的面积为( )
)处的切线与两坐标轴围成的三角形的面积为( )
A.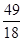 B.
B.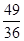 C.
C.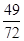 D.
D.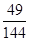
 x3+
x3+ x2在点T(1,
x2在点T(1, )处的切线与两坐标轴围成的三角形的面积为( )
)处的切线与两坐标轴围成的三角形的面积为( )A. | B. | C. | D. |
解答题:解答应写出文字说明,证明过程或演算步骤.
定义F(x,y)=(1+x)y,x,y∈(0,+∞),
(Ⅰ)令函数f(x)=F(1,log2(x2-4x+9))的图象为曲线C1,曲线C1与y轴交于点A(0,m),过坐标原点O向曲线C1作切线,切点为B(n,t)(n>0),设曲线C1在点A、B之间的曲线段与线段OA、OB所围成图形的面积为S,求S的值;
(Ⅱ)令函数g(x)=F(1,log2(x3+ax2+bx+1))的图象为曲线C2,若存在实数b使得曲线C2在x0(-4<x0<-1)处有斜率为-8的切线,求实数a的取值范围;
(Ⅲ)当![]() 且x<y时,证明F(x,y)>F(y,x).
且x<y时,证明F(x,y)>F(y,x).
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com