如图.已知正方体ABCD-A1B1C1D1的棱长为1.E.F分别在棱AB.BC上.G在对角线BD1上.且AE＝.BF＝.D1G∶GB＝1∶2.求平面EFG与底面ABCD所成的二面角的大小. 解析:设G在底面ABCD上的射影为H.H∈BD. ∵＝＝ ∴GH＝ 作HM⊥EF于M.连GM.由三垂线定理知GM⊥EF.则∠GMH＝θ就是平面BFG与底面ABCD所成的二面角的平面角.tanθ＝. 下面求HM的值. 建立如图所示的直角坐标系.据题设可知. H(.).E(.0).F(1.) ∴直线EF的方程为 ＝. 即 4x-6y-1＝0. 由点到直线的距离公式可得 |HM|＝＝. ∴tgθ＝·＝.θ＝arctg. 说明 运用解析法来求HM的值是本例的巧妙所在. 【
查看更多】
题目列表(包括答案和解析)
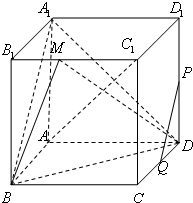
如图，已知正方体ABCD-A
1B
1C
1D
1的棱长为1．P，Q分别是棱DD
1，CD的中点．
（1）证明：AC
1⊥平面A
1BD；PQ∥平面A
1BD；
（2）探究：在棱B
1C
1上是否存在点M，使得二面角M-BD-A
1的大小为45°？若存在，则求出B
1M的值；若不存在，请说明理由．
查看答案和解析>>
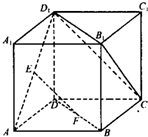
如图，已知正方体ABCD-A
1B
1C
1D
1的棱长为1，E、F分别为AD
1、BD的中点．
（1）求证：EF∥平面B
1D
1C；
（2）求二面角B
1-D
1C-A的大小；
（3）求三棱锥B
1-ACD
1的体积．
查看答案和解析>>
如图，已知正方体ABCD-A
1B
1C
1D
1的棱长为1，点P在棱BB
1上运动（不含B，B
1两点），求△APC
1的面积S的最小值．
查看答案和解析>>
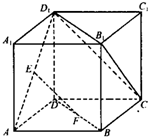如图，已知正方体ABCD-A1B1C1D1的棱长为1，E、F分别为AD1、BD的中点．
（1）求证：EF∥平面B1D1C；
（2）求二面角B1-D1C-A的大小；
（3）求三棱锥B1-ACD1的体积．
查看答案和解析>>
如图，已知正方体ABCD-A1B1C1D1的棱长为1．P，Q分别是棱DD1，CD的中点．
（1）证明：AC1⊥平面A1BD；PQ∥平面A1BD；
（2）探究：在棱B1C1上是否存在点M，使得二面角M-BD-A1的大小为45°？若存在，则求出B1M的值；若不存在，请说明理由．
查看答案和解析>>
