
题目列表(包括答案和解析)
如图9-44,以等腰直角三角形的斜边BC上的高AD为折痕,使△ABD和△ACD折成相垂直的两个面.求证:BD⊥CD,∠BAC=60°.
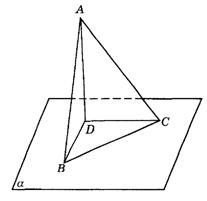
图9-44
| 2 |
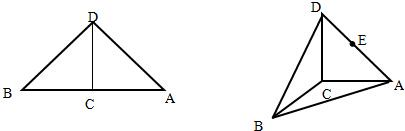
 (2012•福建模拟)在直角梯形ABCD中,AD∥BC,BC=2AD=2AB=2
(2012•福建模拟)在直角梯形ABCD中,AD∥BC,BC=2AD=2AB=2| 2 |
| BN |
| BC |
| 3 |
| BN |
| BC |
 (2013•许昌二模)在直角梯形ABCD中,AD∥BC,AB=1,AD=
(2013•许昌二模)在直角梯形ABCD中,AD∥BC,AB=1,AD=| 3 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com