
题目列表(包括答案和解析)
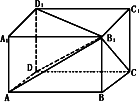
长方体的一条对角线与一个顶点上的三条棱所成的角分别为α、β、γ.
求证:cos2α+cos2β+cos2γ=1
给出以下结论:
①有两个侧面是矩形的棱柱是直棱柱;
②各侧面都是正方形的棱柱一定是正棱柱;
③对角面都是全等的矩形的直四棱柱一定是长方体;
④一个三棱锥四个面可以都为直角三角形;
⑤长方体一条对角线与同一个顶点的三条棱所成的角为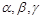 ,则
,则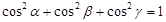 .
.
其中正确的是 .(将正确结论的序号全填上)
给出以下结论:
①有两个侧面是矩形的棱柱是直棱柱;
②各侧面都是正方形的棱柱一定是正棱柱;
③对角面都是全等的矩形的直四棱柱一定是长方体;
④一个三棱锥四个面可以都为直角三角形;
⑤长方体一条对角线与同一个顶点的三条棱所成的角为 ,则
,则 .
.
其中正确的是 .(将正确结论的序号全填上)
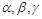 ,则
,则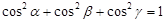 .
.给出以下结论:
①有两个侧面是矩形的棱柱是直棱柱.
②各侧面都是正方形的棱柱一定是正棱柱.
③对角面都是全等的矩形的直四棱柱一定是长方体.
④一个三棱锥四个面可以都为直角三角形.
⑤长方体一条对角线与同一个顶点的三条棱所成的角为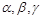 ,则
,则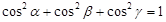
其中正确的是 .(将正确结论的序号全填上)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com