
题目列表(包括答案和解析)
如图,已知曲线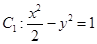 ,曲线
,曲线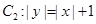 ,P是平面上一点,若存在过点P的直线与
,P是平面上一点,若存在过点P的直线与 都有公共点,则称P为“C1—C2型点”.
都有公共点,则称P为“C1—C2型点”.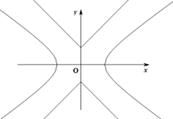
(1)在正确证明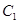 的左焦点是“C1—C2型点”时,要使用一条过该焦点的直线,试写出一条这样的直线的方程(不要求验证);
的左焦点是“C1—C2型点”时,要使用一条过该焦点的直线,试写出一条这样的直线的方程(不要求验证);
(2)设直线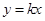 与
与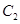 有公共点,求证
有公共点,求证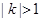 ,进而证明原点不是“C1—C2型点”;
,进而证明原点不是“C1—C2型点”;
(3)求证:圆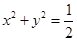 内的点都不是“C1—C2型点”.
内的点都不是“C1—C2型点”.
如图,已知曲线 ,曲线
,曲线 ,P是平面上一点,若存在过点P的直线与
,P是平面上一点,若存在过点P的直线与 都有公共点,则称P为“C1—C2型点”.
都有公共点,则称P为“C1—C2型点”.

(1)在正确证明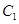 的左焦点是“C1—C2型点”时,要使用一条过该焦点的直线,试写出一条这样的直线的方程(不要求验证);
的左焦点是“C1—C2型点”时,要使用一条过该焦点的直线,试写出一条这样的直线的方程(不要求验证);
(2)设直线 与
与 有公共点,求证
有公共点,求证 ,进而证明原点不是“C1—C2型点”;
,进而证明原点不是“C1—C2型点”;
(3)求证:圆 内的点都不是“C1—C2型点”.
内的点都不是“C1—C2型点”.
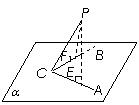 如图,∠ACB = 90°,P是平面ABC外一点,PC = 4cm,点P到角两边AC,BC的距离均为
如图,∠ACB = 90°,P是平面ABC外一点,PC = 4cm,点P到角两边AC,BC的距离均为![]() ,则PC与平面ABC所成角的大小为 .
,则PC与平面ABC所成角的大小为 .

图
求证: a12+a22+a32=b12+b22+b32.
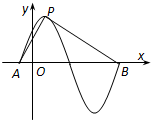 函数y=sin(πx+φ)(φ>0)的部分图象如图所示,设P是图象的最高点,A,B是图象与x轴的交点,记∠APB=θ,则sin2θ的值是( )
函数y=sin(πx+φ)(φ>0)的部分图象如图所示,设P是图象的最高点,A,B是图象与x轴的交点,记∠APB=θ,则sin2θ的值是( )湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com