练习册

  • 练习册
  • 试题
    如图9-20.在空间四边形ABCD中.E是边AB上的一点.求作过C.E的一个平面.使对角线BD平行于这个平面.并说明理由． 解析:在△ABD内过E点作BD的平行线.交AD于F．连结CE.CF.则BD∥平面CEF．∵BD∥EF.BD平面CEF.EF平面CEF.由直线与平面平行的判定定理可知BD∥平面CEF． 【查看更多】

     

    题目列表(包括答案和解析)

    精英家教网如图，已知，在空间四边形ABCD中，BC=AC，AD=BD，E是AB的中点．
    （1）求证：平面CDE⊥平面ABC；
    （2）若AB=DC=3，BC=5，BD=4，求几何体ABCD的体积；
    （3）若G为△ADC的重心，试在线段AB上找一点F，使得GF∥平面CDE．

    查看答案和解析>>

    如图1，椭圆
    x2
    9
    +
    y2
    4
    =1    的下顶点为C，A，B分别在椭圆的第一象限和第二象限的弧上运动，满足
    OA
    ⊥
    OB
    ，其中O为坐标原点，现沿x轴将坐标平面折成直二面角．如图2所示，在空间中，解答下列问题：
    （1）证明：OC⊥AB；
    （2）设二面角O-BC-A的平面角为α，二面角O-AC-B的平面角为β，二面角O-AB-C的平面角为θ，求证：cos2α+cos2β+cos2θ=1；
    （3）求三棱锥O-ABC的体积的最小值．

    查看答案和解析>>

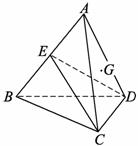
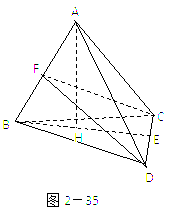    如图2－35：在空间四边形ABCD中，已知BC＝AC，AD＝BD，引BE⊥CD，E为垂足，作AH⊥BE于H，求证：AH⊥平面BCD。

    查看答案和解析>>

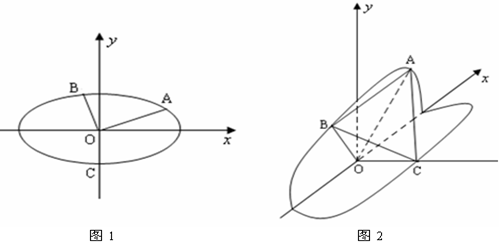
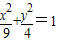    如图1，椭圆的下顶点为C，A，B分别在椭圆的第一象限和第二象限的弧上运动，满足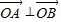，其中O为坐标原点，现沿x轴将坐标平面折成直二面角．如图2所示，在空间中，解答下列问题：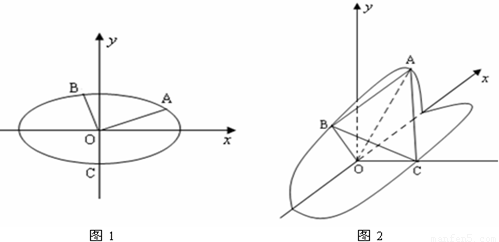
    （1）证明：OC⊥AB；
    （2）设二面角O-BC-A的平面角为α，二面角O-AC-B的平面角为β，二面角O-AB-C的平面角为θ，求证：cos2α+cos2β+cos2θ=1；
    （3）求三棱锥O-ABC的体积的最小值．

    查看答案和解析>>

    如图，已知，在空间四边形中，，是的中点.

    （1）求证：平面⊥平面；

    （2）若,求几何体的体积；

    （3）若为△的重心，试在线段上找一点，使得∥平面.

    查看答案和解析>>


    同步练习册答案