
题目列表(包括答案和解析)
如图(1)所示,将边长为1的正六边形铁皮的六个角各切去一个全等的四边形,再沿虚线折起,做成一个无盖的正六棱柱容器,如图(2)所示,求这个正六棱柱容器容积的最大值.
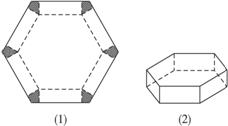
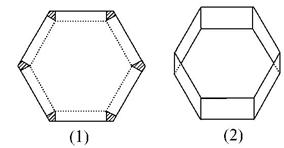
09年湖北鄂州5月模拟文)(12分)如图所示,将边长为2的正三角形铁皮的三个角各切去一个全等的四边形,再沿虚线折起,做成一个无盖的正三棱柱容器,要求正三棱柱容器的高x与底面边长之比不超过正常数t.
⑴把正三棱柱容器的容积V表示为x的函数,并写出函数的定义域;
⑵x为何值时,容积V最大?并求最大值.

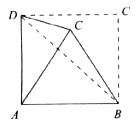
如图所示,将边长为![]() 的正方形ABCD沿对角线BD折成直二面角,若点P满足
的正方形ABCD沿对角线BD折成直二面角,若点P满足![]() ,则
,则![]() 的值为
的值为
A.![]() B.2 C.
B.2 C.![]() D.
D.![]()
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com