
题目列表(包括答案和解析)
数列 首项
首项 ,前
,前 项和
项和 满足等式
满足等式 (常数
(常数 ,
, ……)
……)
(1)求证: 为等比数列;
为等比数列;
(2)设数列 的公比为
的公比为 ,作数列
,作数列 使
使 (
( ……),求数列
……),求数列 的通项公式.
的通项公式.
(3)设 ,求数列
,求数列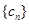 的前
的前 项和
项和 .
.
【解析】第一问利用由 得
得
两式相减得
故 时,
时,
从而 又
又 即
即 ,而
,而
从而 故
故
第二问中,
 又
又 故
故 为等比数列,通项公式为
为等比数列,通项公式为
第三问中,
 两边同乘以
两边同乘以
利用错位相减法得到和。
(1)由 得
得
两式相减得
故 时,
时,
从而 ………………3分
………………3分
又 即
即 ,而
,而
从而 故
故
 对任意
对任意 ,
, 为常数,即
为常数,即 为等比数列………………5分
为等比数列………………5分
(2)
 ……………………7分
……………………7分
又 故
故 为等比数列,通项公式为
为等比数列,通项公式为 ………………9分
………………9分
(3)
 两边同乘以
两边同乘以
 ………………11分
………………11分
两式相减得

(本小题满分14分) 计算下列各式的值:
(1) ![]()
![]() ;(7分)
;(7分)![]()
(2)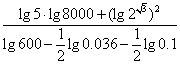 .(7分)
.(7分)
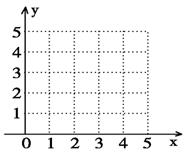
某车间为了规定工时定额,需要确定加工零件所花费的时间,为此作了四次试验如下:
|
零件的个数 |
2 |
3 |
4 |
5 |
|
加工的时间 |
2.5 |
3 |
4 |
4.5 |
(1)在给定坐标系中画出表中数据的散点图;
(2)求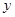 关于
关于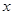 的线性回归方程
的线性回归方程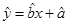 ;
;
(3)试预测加工10个零件需要多少时间?
(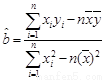 ,
,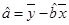 )
)
【解析】第一问中,利用表格中的数据先作出散点图
第二问中,求解均值a,b的值,从而得到线性回归方程。
第三问,利用回归方程将x=10代入方程中,得到y的预测值。
解:(1)散点图(略) (2分)
(2)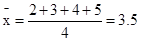
 (4分)
(4分)

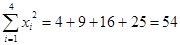 ∴
∴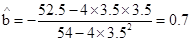 (7分)
(7分)
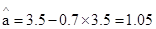 (8分)∴回归直线方程:
(8分)∴回归直线方程: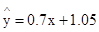 (9分)
(9分)
(3)当 ∴预测加工10个零件需要8.05小时。
∴预测加工10个零件需要8.05小时。
(本小题满分14分) 计算下列各式的值:
(1) ![]()
![]() ;(7分)
;(7分)![]()
(2)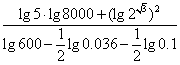 .(7分)
.(7分)
(本小题满分14分) 计算下列各式的值:
(1) ![]()
![]() ;(7分)
;(7分)![]()
(2)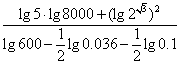 .(7分)
.(7分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com