已知数列{an}满足a1＝0.a2＝2.且对任意m.n∈N*都有 a2m-1+a2n-1＝2am+n-1+2(m-n)2 (Ⅰ)求a3.a5, (Ⅱ)设bn＝a2n+1-a2n-1(n∈N*).证明:{bn}是等差数列, (Ⅲ)设cn＝(an+1-an)qn-1(q≠0.n∈N*).求数列{cn}的前n项和Sn. 本小题主要考查数列的基础知识和化归.分类整合等数学思想.以及推理论证.分析与解决问题的能力. 解:(1)由题意.零m＝2,n-1,可得a3＝2a2-a1+2＝6 再令m＝3,n＝1.可得a5＝2a3-a1+8＝20------------2分 (2)当n∈N *时.由已知(以n+2代替m)可得 a2n+3+a2n-1＝2a2n+1+8 于是[a2(n+1)+1-a2(n+1)-1]-(a2n+1-a2n-1)＝8 即 bn+1-bn＝8 所以{bn}是公差为8的等差数列------------------5分 解答可知{bn}是首项为b1＝a3-a1＝6,公差为8的等差数列 则bn＝8n-2.即a2n+=1-a2n-1＝8n-2 另由已知(令m＝1)可得 an＝-(n-1)2. 那么an+1-an＝-2n+1 ＝-2n+1 ＝2n 于是cn＝2nqn-1. 当q＝1时.Sn＝2+4+6+--+2n＝n(n+1) 当q≠1时.Sn＝2·q0+4·q1+6·q2+--+2n·qn-1. 两边同乘以q.可得 qSn＝2·q1+4·q2+6·q3+--+2n·qn. 上述两式相减得 (1-q)Sn＝2(1+q+q2+--+qn-1)-2nqn ＝2·-2nqn ＝2· 所以Sn＝2· 综上所述.Sn＝----------12分 【
查看更多】
题目列表(包括答案和解析)
已知数列{a
n}满足a
1=，且对任意n∈N
*，都有
=．
（1）求证：数列{
}为等差数列，并求{a
n}的通项公式；
（2）令b
n=a
n•a
n+1，T
n=b
1+b
2+b
3+…+b
n，求证：
Tn＜．
查看答案和解析>>
已知数列{a
n}满足a
n+an+1=(n∈N+)，a
1=-，S
n是数列{a
n}的前n项和，则S
2013=
．
查看答案和解析>>
已知数列{a
n}满足
++…+=n2+n(n∈N*)．
（I）求数列{a
n}的通项公式；
（II）求数列{a
n}的前n项和S
n．
查看答案和解析>>
已知数列{a
n}满足a
1=，且对任意n∈N
+，都有
=．
（1）求{a
n}的通项公式；
（2）令b
n=a
n•a
n+1，T
n=b
1+b
2+b
3+…+b
n，求证：
Tn＜．
查看答案和解析>>
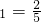，且对任意n∈N+，都有
．
．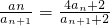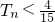