
题目列表(包括答案和解析)
判断题:
(1)
两个长度相等的向量一定相等;[
](2)
相等的向量起点必相同;[
](3)
平行向量就是共线向量;[
](4)
若向量a的模小于b的模,则a<b;[
](5)
质量、动量、功、加速度都是向量;[
](6)
[
](7)
向量a与b平行,则a与b的方向相同或相反;[
](8)
在△ABC中,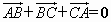 ;
;
[
](9)
若向量a与b有共同的起点,则以b的终点为起点,以a的终点为终点的向量等于b-a;[
](10)
若 且b≠0,当a=
且b≠0,当a=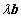 时,则一定有a,b共线;
时,则一定有a,b共线;
[
](11)
若a·b=0,则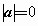 或
或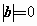 ;
;
[
](12)
若a·b=a·c,且a≠0,则b=c;[
](13)
向量a在b方向上的射影是一个模等于 (
( 是a与b的夹角),方向与b相同或相反的向量;
是a与b的夹角),方向与b相同或相反的向量;
[ ]
(14)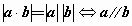 .
.
[
]判断正误:
(正确的用“T”,错误的用“F”.)(1)
在△ABC中,若 ,则△ABC为锐角三角形.
,则△ABC为锐角三角形.
(
)(2)
在△ABC中,若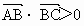 ,则△ABC为钝角三角形.
,则△ABC为钝角三角形.
(
)(3)
在△ABC为直角三角形的充要条件为 .
.
(
)判断正误:(正确的用“T”,错误的用“F”.)
(1)在△ABC中,若 ,则△ABC为锐角三角形.
,则△ABC为锐角三角形.
( )
(2)在△ABC中,若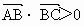 ,则△ABC为钝角三角形.
,则△ABC为钝角三角形.
( )
(3)在△ABC为直角三角形的充要条件为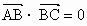 .
.
( )
| 1 |
| 3 |
| AC |
| CB |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com