
题目列表(包括答案和解析)
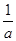 时,f
时,f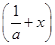 >f
>f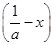 ;
;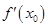 <0.
<0.已知 =(2asin2x,a),
=(2asin2x,a),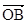 =(-1,2
=(-1,2 sinxcosx+1),O为坐标原点,a≠0,设f(x)=
sinxcosx+1),O为坐标原点,a≠0,设f(x)= ·
·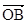 +b,b>a。
+b,b>a。
(1)若a>0,写出函数y=f(x)的单调递增区间;
(2)若函数y=f(x)的定义域为[ ,π],值域为[2,5],求实数a与b的值。
,π],值域为[2,5],求实数a与b的值。
有以下程序:
INPUT x
IF x<=-1 THEN
f(x)=x+2
ELSE IF x>-1 AND x<=1 THEN
f(x)=x x
x
ELSE f(x)=-x+2
END IF
END IF
PRINT f(x)
END
根据如上程序,若函数g(x)=f(x)-m在R上有且只有两个零点,则实数m的取值范围是 .
已知函数f(x)=ax+x2-xlna(a>0,a≠1).
(1)当a>1时,求证:函数f(x)在(0,+∞)上单调递增;
(2)若函数y=|f(x)-t|-1有三个零点,求t的值;
(3)若存在x1、x2∈[-1,1],使得|f(x1)-f(x2)|≥e-1,试求a的取值范围.
已知函数f(x)=lnx-ax2+(2-a)x.
(1)讨论f(x)的单调性;
(2)设a>0,证明:当0<x< 时,f
时,f >f
>f ;
;
(3)若函数y=f(x)的图象与x轴交于A、B两点,线段AB中点的横坐标为x0,证明: <0.
<0.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com