如图.在正三棱柱ABC-A1B1C1中.BB1=2,BC=2.D为B1C1的中点. (Ⅰ)证明:B1C⊥面A1BD, (Ⅱ)求二面角B-AC-B1的大小. 方法一: (Ⅰ)证明:在Rt△BB1D和Rt△B1C1C中. 由 得 △BB1D∽△B1C1C.∠B1DB=∠B1CC1. 又 ∠CB1D+∠B1CC1=90° 故 ∠CB1D+∠B1DB=90° 故 B1C⊥BD.·····················3分 又 正三棱柱ABC-A1B1C1.D为B1C1的中点. 由 A1D⊥平面B1C. 得 A1D⊥B1C 又A1D∩B1D=D. 所以 B1C⊥面A1BD.···················································6分 (Ⅱ)解:设E为AC的中点.连接BE.B1E. 在正三棱柱ABC-A1B1C1中.B1C=B1A.∴B1E⊥AC.BE⊥AC. 即 ∠BEB1为二面角B-AC-B1的平面角·································9分 又 故 所以 二面角的大小为······································12分 方法二: (Ⅰ)证明:设BC的中点为O.如图建立空间直角坐标系O-xyz 依题意有 则 由 故 又 所以 故 又 BD∩BA1=B 所以 B1C⊥面A1BD. (Ⅱ)依题意有 设⊥平面ACB1.⊥平面ABC. 求得 故 所以 二面角的大小为······································12分 【
查看更多】
题目列表(包括答案和解析)

(2013•上海)如图,在正三棱柱ABC-A
1B
1C
1中,AA
1=6,异面直线BC
1与AA
1所成角的大小为
,求该三棱柱的体积.
查看答案和解析>>
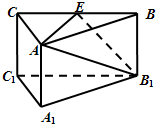
如图,在正三棱柱ABC-A
1B
1C
1中,E是BC中点,则下列叙述正确的是( )
查看答案和解析>>
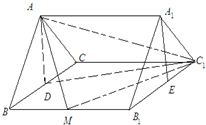
如图,在正三棱柱ABC-A
1B
1C
1中,点D在棱BC上,AD⊥C
1D,
(1)设点M是棱BB
1的中点,求证:平面AMC
1⊥平面AA
1C
1C;
(2)设点E是B
1C
1的中点,过A
1E作平面α交平面ADC
1于l,求证:A
1E∥l.
查看答案和解析>>

如图,在正三棱柱ABC-A
1B
1C
1中,点D在棱BC上,AD⊥C
1D.
(1)求证:AD⊥平面BCC
1B
1;
(2)设点E是B
1C
1的中点,求证:A
1E∥平面ADC
1.
(3)设点M在棱BB
1上,试确定点M的位置,使得平面AMC
1⊥平面AA
1C
1C.
查看答案和解析>>

如图,在正三棱柱ABC-A
1B
1C
1中,底面边长为a,D为BC中点,M在BB
1上,且BM=
B
1M,又CM⊥AC
1.
(1)求证:CM⊥C1D;
(2)求四面体B
1-ADC
1的体积.
查看答案和解析>>

 (2013•上海)如图,在正三棱柱ABC-A1B1C1中,AA1=6,异面直线BC1与AA1所成角的大小为
(2013•上海)如图,在正三棱柱ABC-A1B1C1中,AA1=6,异面直线BC1与AA1所成角的大小为 如图,在正三棱柱ABC-A1B1C1中,E是BC中点,则下列叙述正确的是( )
如图,在正三棱柱ABC-A1B1C1中,E是BC中点,则下列叙述正确的是( ) 如图,在正三棱柱ABC-A1B1C1中,点D在棱BC上,AD⊥C1D,
如图,在正三棱柱ABC-A1B1C1中,点D在棱BC上,AD⊥C1D, 如图,在正三棱柱ABC-A1B1C1中,点D在棱BC上,AD⊥C1D.
如图,在正三棱柱ABC-A1B1C1中,点D在棱BC上,AD⊥C1D. 如图,在正三棱柱ABC-A1B1C1中,底面边长为a,D为BC中点,M在BB1上,且BM=
如图,在正三棱柱ABC-A1B1C1中,底面边长为a,D为BC中点,M在BB1上,且BM=